Question

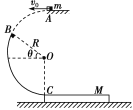
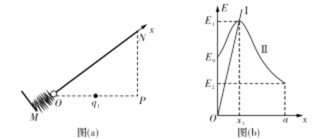
【题目】如图(a)，O、N、P为直角三角形的三个顶点，∠NOP=37°，OP中点处固定一电量为q1 =2.0×10-8 C的正点电荷，M点固定一轻质弹簧。MN是一光滑绝缘杆，其中ON长为a=1 m，杆上穿有一带正电的小球（可视为点电荷），将弹簧压缩到O点由静止释放，小球离开弹簧后到达N点的速度为零。沿ON方向建立坐标轴（取0点处x=0），分别取适当位置为重力势能和电势能的零势能点，图(b)中图线分别为小球的重力势能（以0点为零势能点）和电势能随位置坐标x变化的图象，其中E0=1.15×10-3 J，E1=1. 92×l0-3 J，E2=6.39×10-4J。（静电力常量k=9.0×109 N．m2/C2，取sln 37°=0.6，cos 37°=0.8，重力加速度g=10 m/s2）

(1)求电势能为E时小球的位置坐标x1和小球的质量m；

(2)已知在x1处时小球与杆间的弹力恰好为零，小球已经脱离弹簧，求小球经过此位置时的加速度及小球所带的电荷量q2；

(3)求小球释放瞬间弹簧的弹性势能Ep；

(4)求小球经过x1处时具有的动能Ek。

Answer 1

【答案】(1)；；(2)；；(3)；(4)

【解析】

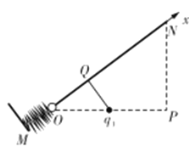
(1)电势能为时最大，所以应是电荷 对小球做负功和正功的分界点，即应该是图中Q（过作的ON的垂线）。

根据图象得到

(2)小球受到重力G、库仑力F，其合力沿杆向下。

故小球的加速度为

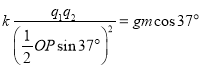
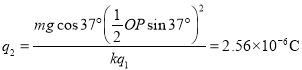
(3)对O到N，小球离开弹簧后到达N点的速度为零，根据能量守恒，得到

(4)根据能量守恒有