题目内容
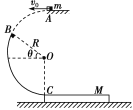
【题目】如图所示,半径R=1.0 m的光滑圆弧轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与水平方向间的夹角θ=37°,另一端点C为轨道的最低点。C点右侧的光滑水平面上紧挨C点静止放置一木板,木板质量M=1 kg,上表面与C点等高。质量为m=1 kg的物块(可视为质点)从空中A点以v0=1.2 m/s的速度水平抛出,恰好从轨道的B端沿切线方向进入轨道。取g=10 m/s2。求:
(1)物块经过B点时的速度vB。
(2)物块经过C点时对木板的压力大小。
(3)若木板足够长,物块在木板上相对滑动过程中产生的热量Q。
【答案】(1)![]() (2)
(2)![]() (3)Q=9 J。
(3)Q=9 J。
【解析】
设物块在B点的速度为vB,在C点的速度为vC,从A到B物块做平抛运动,有
![]() 解得:
解得:![]()
(2)从B到C,根据动能定理有
mgR(1+sin θ)=![]()
解得vC=6 m/s
在C点,由牛顿第二定律列式,有
![]() 解得:
解得:![]()
再根据牛顿第三定律得,物块对木板的压力大小![]()
(3)根据动量守恒定律得:(m+M)v=m![]()
根据能量守恒定律有
![]() (m+M)v2+Q=
(m+M)v2+Q=![]()
联立解得Q=9 J。

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目