��Ŀ����
3�� ��ͼ��ʾ�����������Ե�ҽ�����һ���A��B�����壬��ֹ��ˮƽ�����ϣ�A������Ϊm=0.04kg��������Ϊq=+5.0��10-5C��B������ΪM=0.06kg�������磮��������ˮƽ���Ķ�Ħ��������Ϊ��=0.4��t=0ʱ�̣��ռ����ˮƽ���ҵ���ǿ�糡���糡ǿ��ΪE=1.6��104N/C�����˶�������С��������ĵ���û�б仯����
��ͼ��ʾ�����������Ե�ҽ�����һ���A��B�����壬��ֹ��ˮƽ�����ϣ�A������Ϊm=0.04kg��������Ϊq=+5.0��10-5C��B������ΪM=0.06kg�������磮��������ˮƽ���Ķ�Ħ��������Ϊ��=0.4��t=0ʱ�̣��ռ����ˮƽ���ҵ���ǿ�糡���糡ǿ��ΪE=1.6��104N/C�����˶�������С��������ĵ���û�б仯������1��A��B�ļ��ٶȼ�����������Ĵ�С��
��2����t=2s��糡�����ҳ�ǿ��Ϊԭ����һ�룬������Bͣ��ʱ�������ľ��룮
���� ��1���ڵ糡��������A��Bһ�������ȼ����˶������ٶ���ͬ�����������������ţ�ٵڶ������������ļ��ٶȣ�������������A��B�������������
��2����ǰ2s��AB���ȼ����˶�����v=at���2sĩ���ٶȣ�t=2s��糡�����ҳ�ǿ��Ϊԭ����һ�룬��ʱA��B����ʼ���ȼ����˶�����ţ�ٵڶ��������A��B�ļ��ٶȴ�С�����λ�ƹ�ʽ���Bͣ��ʱ�������ľ��룮
��� �⣺��1�����������������ţ�ٵڶ����ɵã�
a=$\frac{qE-�̣�M+m��g}{M+m}$=$\frac{5��1{0}^{-5}��1.6��1{0}^{4}-0.4����0.04+006����10}{0.04+0.06}$=4m/s2
�����B����������ţ�ٵڶ����ɵã�FN-��Mg=Ma
��� FN=��Mg+Ma=0.4��0.6+0.06��4N=0.48N
��2��t=2sʱ��A��B���ٶ�v=at=2��4m/s=8m/s
t=2s��糡�����ҳ�ǿ��Ϊԭ����һ�룬
��ʱA���ȼ����˶��ļ��ٶȴ�С aA=$\frac{qE��+��mg}{m}$=$\frac{5��1{0}^{-5}��0.8��1{0}^{4}+0.4��0.04��10}{0.04}$=14m/s2��
B���ȼ����˶��ļ��ٶ� ${a_B}=ug=4m/{s^2}$
B�ٶȼ�Ϊ���ʱ�� tB=$\frac{v}{{a}_{B}}$=$\frac{8}{4}$=2s
���ٵ����λ�� x=$\frac{{v}^{2}}{2{a}_{B}}$=$\frac{{8}^{2}}{2��4}$=8m
A�ٶȼ�Ϊ���ʱ�� ${t_{A1}}=\frac{v}{a_A}=\frac{8}{14}s$=$\frac{4}{7}$s�����ٵ����λ�� ${x_{A1}}=\frac{v^2}{{2{a_A}}}=\frac{64}{28}m$=$\frac{16}{7}$m
��A�������ȼ����˶��ļ��ٶȴ�С
aA��=$\frac{qE��-��mg}{m}$=$\frac{5��1{0}^{-5}��0.8��1{0}^{4}-0.4��0.04��10}{0.04}$=6m/s2
�������ȼ���ֱ���˶���λ�� xA2=$\frac{1}{2}{a}_{A}�䣨{t}_{B}-{t}_{A1}��^{2}$=$\frac{1}{2}��6����2-\frac{4}{7}��^{2}$=$\frac{300}{49}m$
��A��B���ľ��� $��x={x_{A2}}+{x_B}-{x_{A1}}=\frac{300}{49}+8-\frac{64}{28}=11.8m$
��
��1��A��B�ļ��ٶ���4m/s2����������Ĵ�С��0.48N��
��2����t=2s��糡�����ҳ�ǿ��Ϊԭ����һ�룬����Bͣ��ʱ�������ľ�����11.8m��
���� �������Ĺؼ�����A��B���˶����ɣ��ر���A���˶������ͨ�������������������A���˶���������ţ�ٵڶ����ɺ��˶�ѧ��ʽ������⣮

 ��У����ϵ�д�
��У����ϵ�д�| A�� | ���ӵ������������� | B�� | ���ӵ���������������RF | ||
| C�� | ������֧���������� | D�� | Ħ��������������-��mgR�� |
| A�� | �ڲ�������ʱ���������ʺ�������½��е��� | |
| B�� | �ڲ�������ʱ���������̺�������½��е��� | |
| C�� | �ڲ���δ֪����ʱ��������ѡ����������Բ� | |
| D�� | �ڲ���δ֪����ʱ��������ѡ�����������̽����Բ� |
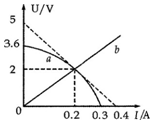 �������һ��̫���ܵ�أ����е�̼�������ŵ㣮��ͼ��ʾ��ͼ��a�Ǹõ����ij����ǿ����·�˵�ѹU�͵���I�Ĺ�ϵͼ������費�dz�������ͼ��b��ij����R��U-Iͼ���ڸù���ǿ���½�������ɱպϻ�·ʱ�������������˵����ȷ���ǣ�������
�������һ��̫���ܵ�أ����е�̼�������ŵ㣮��ͼ��ʾ��ͼ��a�Ǹõ����ij����ǿ����·�˵�ѹU�͵���I�Ĺ�ϵͼ������費�dz�������ͼ��b��ij����R��U-Iͼ���ڸù���ǿ���½�������ɱպϻ�·ʱ�������������˵����ȷ���ǣ�������| A�� | ��ʱ����ص�����Ϊ12.5�� | B�� | ��ʱ����ص��������Ϊ 0.2W | ||
| C�� | ��ʱ����ص��ܹ���Ϊ 0.72W | D�� | ��ʱ����ص����Ч��Ϊ 40% |
 ��ͼ��ʾ���ڹ⻬ˮƽ������ABC����������Ϊm��С��A�����磬B�����磬C�����磬A��B�������ľ���ֵ��ΪQ��B��C����С���þ�Եϸ��������һ�𣬵�������F����A�������˶�ʱ��B��CҲ����A��һ�������˶������˶�����������С����Ծ�ֹ��ͬ�˶���������
��ͼ��ʾ���ڹ⻬ˮƽ������ABC����������Ϊm��С��A�����磬B�����磬C�����磬A��B�������ľ���ֵ��ΪQ��B��C����С���þ�Եϸ��������һ�𣬵�������F����A�������˶�ʱ��B��CҲ����A��һ�������˶������˶�����������С����Ծ�ֹ��ͬ�˶���������| A�� | BC������������СΪ$\frac{2}{3}$F | B�� | BC������������СΪ$\frac{1}{3}$F | ||
| C�� | AB������Ϊ$\sqrt{\frac{3K{Q}^{2}}{2F}}$ | D�� | AB������Ϊ$\sqrt{\frac{3K{Q}^{2}}{F}}$ |
| A�� | ���ʿ˸��ݺ������Ĺ��ɣ�����������ӵĹ۵� | |
| B�� | �����ն�ͨ���о��˿�ʯ����������Ȼ�������� | |
| C�� | �������ݦ�����ɢ��ʵ�飬�����ԭ�ӵĺ�ʽ�ṹģ�� | |
| D�� | ��ķѷͨ���о��������߷����˵��ӣ�����ȷ���������ӵĵ���� |
| A�� | ���˻������˶����ٶȴ�С | B�� | ���˻��ڿ��о���ˮƽ����ĸ߶� | ||
| C�� | С���ڿ����˶���ʱ�� | D�� | ���ص��������ٶ� |
