题目内容
在xOy平面内,x＞0的区域存在垂直纸面向里的匀强磁场,磁感应强度为B=0.4 T;
x＜0的区域存在沿x轴正方向的匀强电场.现有一质量为m=4.0×10-9 kg, 带电荷量为
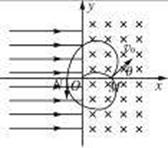
q=2.0×10－7 C的正粒子从x轴正方向上的M点以速度v0=20 m/s进入磁场,如图11-10所示,v0与x轴正方向的夹角θ=45°,M点与O点相距为l=
m.已知粒子能以沿着y轴负方向的速度垂直穿过x轴负半轴上的N点,不计粒子重力.求:
(1)粒子穿过y轴正半轴的位置以及此时速度与y轴负方向的夹角;
(2)x＜0区域电场的场强;
(3)试问粒子能否经过坐标原点O?若不能,请说明原因;若能,请求出粒子从M点运动到O点所经历的时间.
解析:(1)粒子在磁场中做匀速圆周运动时,由洛伦兹力提供向心力
Bqv0=mv02/R 得:R=1 m （2分）
过M点做初速度v0的垂线交y轴正方向于P点,则PM=l/cos45°
得:PM=2 m=2R （1分）
由几何关系得PM为轨迹圆的直径,P点即为粒子穿过y轴正半轴的位置
（2分）
由圆的对称性得粒子经过此处时的速度与y轴负方向的夹角为θ=45°. （1分）
(2)设粒子由P点到N点历时t1,则:
x轴方向:v0sin45°－Eqt1/m=0 （2分）
y轴方向:v0t1cos45°=OP （2分）
联立求解,代入数据得:t1=0.1 s,
（2分）
(3)粒子能到达O点
粒子在磁场中的运动周期为:T=2πm/Bq
从M点运动到O点经过的轨迹如图
经历的时间为:t=T/2+3T/4+2t1
代入数据得: t=(π/8+0.2) s≈0.59 s. （6分）
答案:(1)45° (2)2.82 V/m (3)0.59 s
练习册系列答案
阅读快车系列答案
相关题目
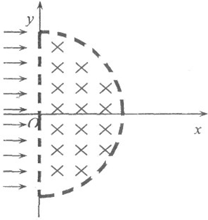（2011?绍兴二模）如图所示，在xoy平面内x＞0处有一半圆形匀强磁场，磁场区域圆心为O，半径为R=0.10m，磁感应强度大小为B=0.5T，磁场方向垂直xoy平面向里．有一线状粒子源放在y轴左侧（图中未画出），不断沿平行于x轴正方向放出电荷量为q=+1.6×10-19C、初速度为v0=1.6×106m/s的粒子，粒子的质量为m=1.0×10-26kg，不考虑粒子间的相互作用，粒子重力忽略不计．求：
m.已知粒子能以沿着y轴负方向的速度垂直穿过x轴负半轴上的N点,不计粒子重力.求:
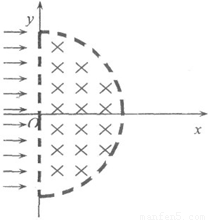如图所示，在xoy平面内x＞0处有一半圆形匀强磁场，磁场区域圆心为O，半径为R=0.10m，磁感应强度大小为B=0.5T，磁场方向垂直xoy平面向里．有一线状粒子源放在y轴左侧（图中未画出），不断沿平行于x轴正方向放出电荷量为q=+1.6×10-19C、初速度为v=1.6×106m/s的粒子，粒子的质量为m=1.0×10-26kg，不考虑粒子间的相互作用，粒子重力忽略不计．求：