题目内容
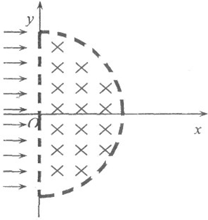 (2011?绍兴二模)如图所示,在xoy平面内x>0处有一半圆形匀强磁场,磁场区域圆心为O,半径为R=0.10m,磁感应强度大小为B=0.5T,磁场方向垂直xoy平面向里.有一线状粒子源放在y轴左侧(图中未画出),不断沿平行于x轴正方向放出电荷量为q=+1.6×10-19C、初速度为v0=1.6×106m/s的粒子,粒子的质量为m=1.0×10-26kg,不考虑粒子间的相互作用,粒子重力忽略不计.求:
(2011?绍兴二模)如图所示,在xoy平面内x>0处有一半圆形匀强磁场,磁场区域圆心为O,半径为R=0.10m,磁感应强度大小为B=0.5T,磁场方向垂直xoy平面向里.有一线状粒子源放在y轴左侧(图中未画出),不断沿平行于x轴正方向放出电荷量为q=+1.6×10-19C、初速度为v0=1.6×106m/s的粒子,粒子的质量为m=1.0×10-26kg,不考虑粒子间的相互作用,粒子重力忽略不计.求:(1)从O点入射的粒子离开磁场区域的y轴坐标;
(2)从y轴任意位置(0,y)入射的粒子在离开磁场时的速度方向与正x轴夹角的余弦值;
(3)这些粒子在该磁场中运动的最长时间,并指出该粒子入射时的坐标.
分析:(1)粒子在磁场中做圆周运动,根据粒子的运动轨迹和几何关系可以求得粒子设出时的位置的坐标;
(2)从任意位置进入磁场时,根据粒子的运动画出粒子的运动的轨迹,再由三角形得关系可以求得速度方向;
(3)粒子在磁场中运动的圆心角越的,粒子在磁场中运动的时间就越长,根据粒子的运动的轨迹的关系,可以求得粒子的运动最长时间的位置.
(2)从任意位置进入磁场时,根据粒子的运动画出粒子的运动的轨迹,再由三角形得关系可以求得速度方向;
(3)粒子在磁场中运动的圆心角越的,粒子在磁场中运动的时间就越长,根据粒子的运动的轨迹的关系,可以求得粒子的运动最长时间的位置.
解答:解:
(1)粒子在磁场中的运动满足
qvB=m
可得粒子的运动的半径为r=
=0.2m
当粒子从O点入射时,画出粒子的运动轨迹圆弧OP,设P点坐标为(xp,yp),则OQ=yp,
故O′Q=r-yp,
由直角三角形△O′PQ关系可得:
x
+(r-yp)2=r2
P点坐标同时满足
+
=R2
联立可得 yp=
,
代入数据得yp=0.025m
(2)如右图,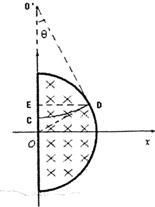 粒子从C点入射,画出其在磁场中运动的轨迹,交与磁场边界D点,并画出其运动轨迹的圆心O,
粒子从C点入射,画出其在磁场中运动的轨迹,交与磁场边界D点,并画出其运动轨迹的圆心O,
设弧CD所对圆心为θ,过D点做x轴的平行线交y轴与E点,连接OD,
则OO′=r+y
由直角三角形△O′ED得,O′E=rcosθ,DE=rsinθ
则OE=O′O-O′E=r+y-rcosθ
在直角三角形△OED内,有OE2+DE2=OD2
代入得 (r+y-rcos)2+(rsinθ)2=R2
可求得 cosθ=
,
代入数据得 cosθ=
,
(3)由 cosθ=
,
变式得:cosθ=
+
,
这说明当
=
时,cosθ具有最小值,θ具有最大值.
代入数据得y=0.1
-0.2≈-0.027
即入射点在x轴下方做标为(0,-0.027)处
此时cosθ=0.5
即θ=
由周期公式T=
得tm=
=
π×10-7s≈2.1×10-7s.

(1)粒子在磁场中的运动满足
qvB=m
| ||
| r |
可得粒子的运动的半径为r=
| mv0 |
| qB |
当粒子从O点入射时,画出粒子的运动轨迹圆弧OP,设P点坐标为(xp,yp),则OQ=yp,
故O′Q=r-yp,
由直角三角形△O′PQ关系可得:
x
2 p |
P点坐标同时满足
| x | 2 p |
| y | 2 p |
联立可得 yp=
| R2 |
| 2r |
代入数据得yp=0.025m
(2)如右图,
 粒子从C点入射,画出其在磁场中运动的轨迹,交与磁场边界D点,并画出其运动轨迹的圆心O,
粒子从C点入射,画出其在磁场中运动的轨迹,交与磁场边界D点,并画出其运动轨迹的圆心O,设弧CD所对圆心为θ,过D点做x轴的平行线交y轴与E点,连接OD,
则OO′=r+y
由直角三角形△O′ED得,O′E=rcosθ,DE=rsinθ
则OE=O′O-O′E=r+y-rcosθ
在直角三角形△OED内,有OE2+DE2=OD2
代入得 (r+y-rcos)2+(rsinθ)2=R2
可求得 cosθ=
| (r+y)2+r2-R2 |
| 2(r+y)r |
代入数据得 cosθ=
| 10y2+4y+0.7 |
| 4y+0.8 |
(3)由 cosθ=
| (r+y)2+r2-R2 |
| 2(r+y)r |
变式得:cosθ=
| r+y |
| 2r |
| r2-R2 |
| 2r(r+y) |
这说明当
| r+y |
| 2r |
| r2-R2 |
| 2r(r+y) |
代入数据得y=0.1
| 3 |
即入射点在x轴下方做标为(0,-0.027)处
此时cosθ=0.5
即θ=
| π |
| 3 |
由周期公式T=
| 2πm |
| qB |
得tm=
| θm |
| qB |
| 2 |
| 3 |
点评:电荷在匀强磁场中做匀速圆周运动,关键是画出轨迹,由几何知识求出半径.定圆心角,求时间.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011?绍兴二模)如图所示,水平固定倾角为30°的光滑斜面上有两质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧连接,现对B施加一水平向右推力F使A、B均静止在斜面上,此时弹簧的长度为l,则弹簧原长和推力为F的大小分别为( )
(2011?绍兴二模)如图所示,水平固定倾角为30°的光滑斜面上有两质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧连接,现对B施加一水平向右推力F使A、B均静止在斜面上,此时弹簧的长度为l,则弹簧原长和推力为F的大小分别为( ) (2011?绍兴二模)某同学在家中用三根相同的橡皮筋(遵循胡克定律)来探究求合力的方法.如图所示,三根橡皮筋在O点相互连接,拉长后三个端点用图钉固定在A、B、C三点.在实验中,可以通过刻度尺测量橡皮筋的长度来得到橡皮筋的拉力大小,并通过OA、OB、OC的方向确定三个拉力的方向,从而探究求其中任意两个拉力的合力的方法.在实验过程中,下列说法正确的是( )
(2011?绍兴二模)某同学在家中用三根相同的橡皮筋(遵循胡克定律)来探究求合力的方法.如图所示,三根橡皮筋在O点相互连接,拉长后三个端点用图钉固定在A、B、C三点.在实验中,可以通过刻度尺测量橡皮筋的长度来得到橡皮筋的拉力大小,并通过OA、OB、OC的方向确定三个拉力的方向,从而探究求其中任意两个拉力的合力的方法.在实验过程中,下列说法正确的是( )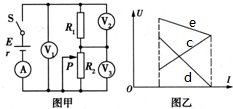 (2011?绍兴二模)在如图a所示电路中,闭合电键S,当滑动变阻器的滑动触头P向下滑动的过程中,四个理想电表的示数都发生变化.图b中三条图线分别表示了三个电压表示数随电流的变化的情况.下列说法正确是( )
(2011?绍兴二模)在如图a所示电路中,闭合电键S,当滑动变阻器的滑动触头P向下滑动的过程中,四个理想电表的示数都发生变化.图b中三条图线分别表示了三个电压表示数随电流的变化的情况.下列说法正确是( )