题目内容
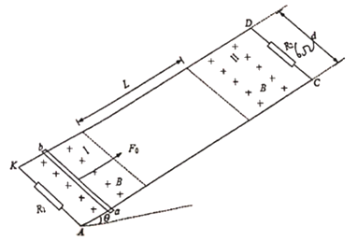
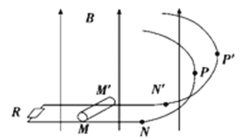
【题目】如图所示,光滑、平行的金属轨道分水平段(左端接有阻值为R的定值电阻)和半圆弧段两部分,两段轨道相切于N和N′点,圆弧的半径为r=0.4m,两金属轨道间的宽度为d=0.4m,整个轨道处于磁感应强度为B=0.5T,方向竖直向上的匀强磁场中。质量为m=0.2kg、长也为d、电阻也为R的金属细杆置于框架上的MM′处,MN=d。在t=0时刻,给金属细杆一个方向垂直金属细杆、水平向右的初速度v0=8m/s,之后金属细杆沿轨道运动,在t=t1时刻,金属细杆以速度v=4m/s通过与圆心等高的P和P′;在t=t2时刻,金属细杆恰好通过圆弧轨道的最高点,金属细杆与轨道始终接触良好,轨道的电阻和空气阻力均不计,其中重力加速度为g=10m/s2,R=1Ω。以下说法正确的是( )
A.t=t1时刻,金属细杆所受的安培力为![]()
B.从t=0到t=t1时刻,通过金属细杆横截面的电量为![]()
C.t=0时刻,金属细杆两端的电压为1.6V
D.从t=0到t=t2时刻,定值电阻R产生的焦耳热为2.2J
【答案】BD
【解析】
A.![]() 时刻,金属细杆的速度与磁场平行,不切割磁感线,不产生感应电流,所以杆不受安培力,故A错误;
时刻,金属细杆的速度与磁场平行,不切割磁感线,不产生感应电流,所以杆不受安培力,故A错误;
B.从![]() 到
到![]() 时刻,通过金属细杆横截面的电量为
时刻,通过金属细杆横截面的电量为
![]()
B正确;
C.![]() 时刻,金属细杆产生的感应电动势为
时刻,金属细杆产生的感应电动势为
![]()
两端的电压为
![]()
C错误;
D.在最高点,有
![]()
解得
![]()
从![]() 到
到![]() 时刻,定值电阻R产生的焦耳热为
时刻,定值电阻R产生的焦耳热为
![]()
代入数据解得
![]()
D正确。
故选BD。

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目