题目内容
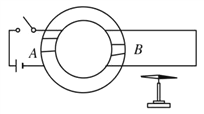
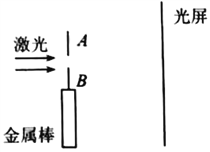
【题目】如图所示，光滑平行导轨仅其水平部分处于竖直向上的匀强磁场中，金属杆b静止在导轨的水平部分上，金属杆a沿导轨的弧形部分从离地h处由静止开始下滑，运动中两杆始终与轨道垂直并接触良好且它们之间未发生碰撞，已知a杆的质量ma=m0，b杆的质量mb=
m0，且水平导轨足够长.
(1)a和b的最终速度分别是多大？
(2)整个过程中回路释放的电能是多少？
(3)若已知a、b杆的电阻之比Ra:Rb=3:4，其余电阻不计，则整个过程中a、b上产生的热量分别是多少？
【答案】(1) 
(2)
m0gh (3)
m0gh
【解析】本题考查电磁感应中的双棒问题，需运用动能定理、动量守恒、功能关系等知识。
(1)以a为研究对象，对a沿导轨的弧形部分下滑h的过程应用动能定理可得：
a沿导轨的水平部分运动过程中切割磁感线，回路中产生感应电流，a受安培力作用减速b受安培力作用加速，当两者速度相等时，电流为零，达到稳定状态。
以a、b两杆为系统，据动量守恒可得
联立解得：
(2)对全过程由功能关系可得，整个过程中回路释放的电能
，解得：
(3)流过a、b两杆的电流始终相等，两杆a、b上产生的热量之比
，又
，解得：
、
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
