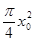题目内容
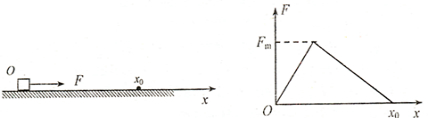
静置于光滑水平面上坐标原点处的小物块,在水平拉力F作用下,沿x轴方向运动,拉力F随物块所在位置坐标x的变化关系如图所示,图线为两段直线.则小物块运动到x0处时的动能为
.
| Fmx0 |
| 2 |
| Fmx0 |
| 2 |

分析:根据F-x图象的“面积”求出拉力F做的功,再根据动能定理求解小物块运动到x0处时的动能.
解答:解:F-x图象的“面积”等于拉力做功的大小,则得到拉力做功等于三角形的面积:W=
Fm?x0,由动能定理得:小物块运动到x0处时的动能为Ek=W=
故答案为:
| 1 |
| 2 |
| Fmx0 |
| 2 |
故答案为:
| Fmx0 |
| 2 |
点评:本题关键抓住F-x图象的“面积”等于拉力做功的大小去理解和分析.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
如图甲所示,静置于光滑水平面上坐标原点O处的小物块,在水平拉力F的作用下沿x轴方向运动,拉力F随物块所在位置坐标x的变化关系如图乙所示,图线为半圆,则小物块运动到x0处时的动能为( )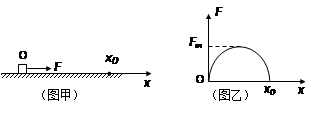
| A.0; | B.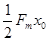 ; ; | C.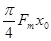 ; ; | D.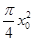 |
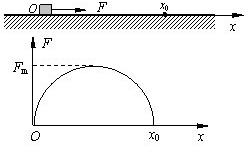 如图甲所示,静置于光滑水平面上坐标原点处的小物块,在水平拉力F作用下,沿x轴方向运动,拉力F随物块所在位置坐标x的变化关系如图乙所示,图线为半圆.则小物块运动到x0处时的动能为( )
如图甲所示,静置于光滑水平面上坐标原点处的小物块,在水平拉力F作用下,沿x轴方向运动,拉力F随物块所在位置坐标x的变化关系如图乙所示,图线为半圆.则小物块运动到x0处时的动能为( )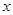 的变化关系如图乙所示,图线为半圆。则小物块运动到
的变化关系如图乙所示,图线为半圆。则小物块运动到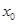 处时的动能为( )
处时的动能为( )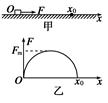
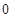 B.
B.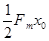 C.
C.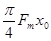 D.
D.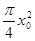
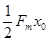
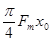 D.
D.