题目内容
【题目】如图所示，一个绝缘且内壁光滑的环形细圆管，固定于竖直平面内，环的半径为R（比细管的内径大得多），在圆管内的最低点有一个直径略小于细管内径的带正电小球处于静止状态，小球的质量为m，带电荷量为q，重力加速度为g．空间存在一磁感应强度大小未知（不为零），方向垂直于环形细圆管所在平面且向里的匀强磁场．某时刻，给小球一方向水平向右，大小为
的初速度，则以下判断正确的是 （ ）
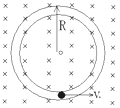
A. 无论磁感应强度大小如何，获得初速度后的瞬间，小球在最低点一定受到管壁的弹力作用
B. 无论磁感应强度大小如何，小球一定能到达环形细管的最高点，且小球在最高点一定受到管壁的弹力作用
C. 无论磁感应强度大小如何，小球一定能到达环形细管的最高点，且小球到达最高点时的速度大小都不同
D. 小球在从环形细圆管的最低点运动到所能到达的最高点的过程中，机械能不守恒
【答案】B
【解析】由左手定则可判断小球受到的洛伦兹力F始终指向圆心，另外假设小球受到管道的支持力N，小球获得
的初速度后，由圆周运动可知：
计算得出：
，即
可见，只要B足够大，满足
，支持力N就可以为零，A错误；
整个过程洛伦兹力不做功，设小球在最高点速度大小为v，则根据动能定理可知
，解得
。
故小球在最高点需要得向心力大小
，所以小球除了受重力，向下得洛伦兹力以外，一定还受轨道向上的支持力，该力和洛伦兹力大小相等，故B正确，C错误；
小球在整个运动过程中，只有重力对其做功，满足机械能守恒得条件，故D错误。
练习册系列答案
相关题目
