题目内容
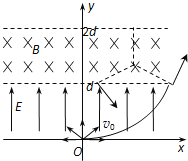
【题目】如图所示，将某正粒子放射源置于原点O，其向各个方向射出的粒子速度大小均为v0，质量均为m、电荷量均为q；在0≤y≤d的一、二象限范围内分布着一个匀强电场，方向与y轴正向相同，在d<y≤2d的一、二象限范围内分布着一个匀强磁场，方向垂直于xoy平面向里．粒子离开电场上边缘y=d时，能够到达的最右侧的位置为（1．5d，d）．最终恰没有粒子从y=2d的边界离开磁场．已知sin37°=0．6，cos37°=0．8，不计粒子重力以及粒子间的相互作用，求：
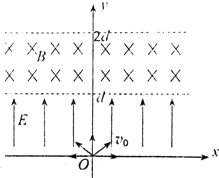
（1）电场强度E；
（2）磁感应强度B；
（3）粒子在磁场中运动的最长时间
【答案】（1）
（2）
（3）
【解析】
试题分析：（1）沿x轴正方向发射的粒子有：x=1．5d，y=d，
由类平抛运动基本规律得：x=v0t，
y＝
at2，
而
，
联立可得：
（2）沿x轴正方向发射的粒子射入磁场时有：1．5d=v0t，
d＝
t，
联立可得：vy＝
v0，
，方向与水平成53°，斜向右上方，
据题意知该粒子轨迹恰与上边缘相切，则其余粒子均达不到y=2d边界，由几何关系可知：
d＝R+
R，
根据牛顿第二定律得：
解得：
联立可得：
（3）粒子运动的最长时间对应最大的圆心角，经过（1．5d，d）恰与上边界相切的粒子轨迹对应的圆心角最大，由几何关系可知圆心角为：θ=254°，
粒子运动周期为：
，
则时间为：
．
【题目】物理小组在一次探究活动中测量滑块与木板之间的动摩擦因数。实验装置如右图所示，一表面粗糙的木板固定在水平桌面上，一端装有定滑轮；木板上有一滑块，其一端与电磁打点计时器的纸带相连，另一端通过跨过定滑轮的细线与托盘连接。打点计时器使用的交流电源的频率为50 Hz。开始实验时，在托盘中放入适量砝码，滑块开始做匀加速运动，在纸带上打出一系列小点。根据图中数据得出滑块的加速度为a。
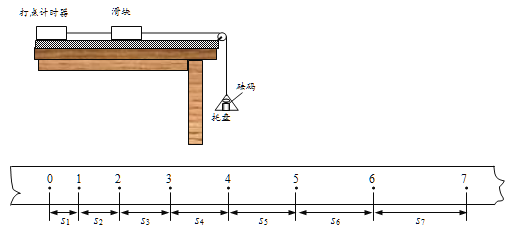
（1）为测量动摩擦因数，下列物理量中还应测量的有 （填入所选物理量前的字母）
A．木板的长度 |
B．木板的质量m1 |
C．滑块的质量m2 |
D．托盘和砝码的总质量m3 |
E．滑块运动的时间t
（2）测量（1）中所选定的物理量时需要的实验器材是 。
（3）滑块与木板间的动摩擦因数μ＝ （用被测物理量的字母表示，重力加速度为g）。
