题目内容
8.一物体在斜面的顶端由静止开始下滑,斜面长10m,高5m,物体与斜面间的滑动摩擦因数是0.02,求物体滑到斜面底端的速度.分析 由几何关系可明确斜面的倾角,再分析受力情况,根据动能定理可求得物体滑到底端时的速度.
解答 解:由几何关系可得sinθ=$\frac{5}{10}$=$\frac{1}{2}$; cosθ=$\frac{\sqrt{3}}{2}$
对下落过程由动能定理可得:
mgh-μmgcosθL=$\frac{1}{2}$mv2
解得:v=9.8m/s
答:物体滑到底部时的速度为9.8m/s.
点评 本题考查动能定理的应用,要注意明确动能定理应用的优点;本题也可以用牛顿第二定律及运动学公式进行分析求解,但过程及计算均显麻烦.

练习册系列答案
相关题目
18.如图是物体做直线运动的v-t图象,由图可知,该物体( )


| A. | 第1s内和第3s内的运动方向相同 | |
| B. | 第3s内和第4s内的加速度相同 | |
| C. | 第1s内和第3s内的位移大小相等 | |
| D. | 0~2s内和0~4s内的平均速度大小相等 |
4.火星和地球质量之比为P,火星和地球的半径之比为q,则火星表面处和地球表面处的重力加速度之比为( )
| A. | $\frac{p}{{q}^{2}}$ | B. | p•q2 | C. | $\frac{p}{q}$ | D. | p•q |
1.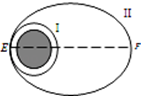 今年5月,信使号水星探测器陨落在水星表面.之前,工程师通过向后释放推进系统中的高压氦气来提升轨道,使其寿命再延长一个月,如图所示,释放氦气前,探测器在贴近水星表面的圆形轨道Ⅰ上做匀速圆周运动,释放氦气后探测器进入椭圆轨道Ⅱ,忽略探测器在椭圆轨道上所受阻力.则下列说法正确的是( )
今年5月,信使号水星探测器陨落在水星表面.之前,工程师通过向后释放推进系统中的高压氦气来提升轨道,使其寿命再延长一个月,如图所示,释放氦气前,探测器在贴近水星表面的圆形轨道Ⅰ上做匀速圆周运动,释放氦气后探测器进入椭圆轨道Ⅱ,忽略探测器在椭圆轨道上所受阻力.则下列说法正确的是( )
 今年5月,信使号水星探测器陨落在水星表面.之前,工程师通过向后释放推进系统中的高压氦气来提升轨道,使其寿命再延长一个月,如图所示,释放氦气前,探测器在贴近水星表面的圆形轨道Ⅰ上做匀速圆周运动,释放氦气后探测器进入椭圆轨道Ⅱ,忽略探测器在椭圆轨道上所受阻力.则下列说法正确的是( )
今年5月,信使号水星探测器陨落在水星表面.之前,工程师通过向后释放推进系统中的高压氦气来提升轨道,使其寿命再延长一个月,如图所示,释放氦气前,探测器在贴近水星表面的圆形轨道Ⅰ上做匀速圆周运动,释放氦气后探测器进入椭圆轨道Ⅱ,忽略探测器在椭圆轨道上所受阻力.则下列说法正确的是( )| A. | 探测器在轨道I的运行周期比在轨道Ⅱ的大 | |
| B. | 探测器在轨道Ⅱ上某点的速率可能等于在轨道Ⅰ上速率 | |
| C. | 探测器在轨道Ⅰ和轨道Ⅱ上的E处加速度相同 | |
| D. | 探测器在轨道Ⅱ上远离水星过程中,势能和动能均增大 |
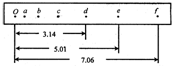 在“验证机械能守恒定律”实验中,质量为0.2kg的重物自由下落,它拖动的纸带上通过电磁打点计时器打出一系列的点O、a、b、c、d、e、f等,如图所示,其中O为打出的第一个点.已知打点计时器所用电源频率为50Hz,图中长度的单位为cm,取g=9.8m/s2.试问:(保留两位有效数字)
在“验证机械能守恒定律”实验中,质量为0.2kg的重物自由下落,它拖动的纸带上通过电磁打点计时器打出一系列的点O、a、b、c、d、e、f等,如图所示,其中O为打出的第一个点.已知打点计时器所用电源频率为50Hz,图中长度的单位为cm,取g=9.8m/s2.试问:(保留两位有效数字) 
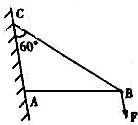 如图所示,AB是一轻杆,BC是一轻绳,在B端施加一作用力F,F的大小为100N,方向竖直向下.试求轻绳受到的拉力和杆受到的压力.(轻绳与墙壁的夹角为60°)
如图所示,AB是一轻杆,BC是一轻绳,在B端施加一作用力F,F的大小为100N,方向竖直向下.试求轻绳受到的拉力和杆受到的压力.(轻绳与墙壁的夹角为60°)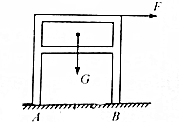 如图所示,桌子在水平力F的作用下匀速缓慢移动,已知桌子重G=100N,桌腿与地面的摩擦系数μ=0.2,桌子的宽、高相等.求:
如图所示,桌子在水平力F的作用下匀速缓慢移动,已知桌子重G=100N,桌腿与地面的摩擦系数μ=0.2,桌子的宽、高相等.求: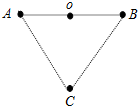 如图所示,A、B是带等量异种电荷Q的带电体,O点是AB连线的中点,C点是AB连线中垂线上的一点,A、B、C构成一个等边三角形,边长为r,则O点场强大小为$\frac{8kQ}{{r}^{2}}$,C点的场强大小为$\frac{kQ}{{r}^{2}}$.
如图所示,A、B是带等量异种电荷Q的带电体,O点是AB连线的中点,C点是AB连线中垂线上的一点,A、B、C构成一个等边三角形,边长为r,则O点场强大小为$\frac{8kQ}{{r}^{2}}$,C点的场强大小为$\frac{kQ}{{r}^{2}}$.