题目内容
2.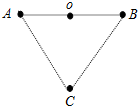 如图所示,A、B是带等量异种电荷Q的带电体,O点是AB连线的中点,C点是AB连线中垂线上的一点,A、B、C构成一个等边三角形,边长为r,则O点场强大小为$\frac{8kQ}{{r}^{2}}$,C点的场强大小为$\frac{kQ}{{r}^{2}}$.
如图所示,A、B是带等量异种电荷Q的带电体,O点是AB连线的中点,C点是AB连线中垂线上的一点,A、B、C构成一个等边三角形,边长为r,则O点场强大小为$\frac{8kQ}{{r}^{2}}$,C点的场强大小为$\frac{kQ}{{r}^{2}}$.
分析 根据点电荷电场强度公式E=$\frac{kQ}{{r}^{2}}$,及几何关系,同时结合矢量叠加法则,即可求解两点的电场强度大小.
解答 解:根据点电荷电场强度公式E=$\frac{kQ}{{r}^{2}}$,则A点在O处的电场强度为EA=$\frac{kQ}{(\frac{r}{2})^{2}}$;
同理,B点在O处的电场强度为EB=$\frac{kQ}{(\frac{r}{2})^{2}}$;
由于A、B是带等量异种电荷,
根据矢量的合成法则,则O点场强大小为E=$\frac{8kQ}{{r}^{2}}$
而A点在C处的电场强度为EA′=$\frac{kQ}{{r}^{2}}$
那么B点在C处的电场强度为EB′=$\frac{kQ}{{r}^{2}}$
因A、B是带等量异种电荷,因此A、B两电荷在C处的电场强度方向夹角为120°
根据矢量的合成法则,则C点场强大小为E=$\frac{kQ}{{r}^{2}}$
故答案为:$\frac{8kQ}{{r}^{2}}$,$\frac{kQ}{{r}^{2}}$.
点评 考查点电荷电场强度的公式的内容,掌握矢量合成法则,理解电场强度的方向与场源电荷的电性关系,同时注意几何关系的正确运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列说法中可能存在的有( )
| A. | 加速度就是增加的速度,它反映了速度变化的大小 | |
| B. | 物体速度变化很大,加速度却很小 | |
| C. | 加速度反映了速度变化的快慢,其方向就是速度变化量的方向 | |
| D. | 速度在增加,加速度却在减小 |
14.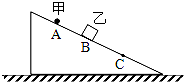 在绝缘粗糙的斜面上A点处固定一点电荷甲,将一带电小物块乙从斜面上B点处由静止释放,乙沿斜面运动到C点处静止,则( )
在绝缘粗糙的斜面上A点处固定一点电荷甲,将一带电小物块乙从斜面上B点处由静止释放,乙沿斜面运动到C点处静止,则( )
 在绝缘粗糙的斜面上A点处固定一点电荷甲,将一带电小物块乙从斜面上B点处由静止释放,乙沿斜面运动到C点处静止,则( )
在绝缘粗糙的斜面上A点处固定一点电荷甲,将一带电小物块乙从斜面上B点处由静止释放,乙沿斜面运动到C点处静止,则( )| A. | 甲、乙一定带同种电荷 | |
| B. | B点的电势一定高于C点的电势 | |
| C. | 从B到C的过程中,乙的电势能一定减少 | |
| D. | 从B到C的过程中,乙的机械能的损失量一定等于克服摩擦力做的功 |
11.关于电场中的等势面,下列说法中正确的有( )
| A. | 等量同种电荷的连线的中垂线是等势线 | |
| B. | 沿电场线方向电势是降低的 | |
| C. | 在同一等势面上两点间移动电荷,电场力做功为零 | |
| D. | 处于静电平衡状态的导体是等势体,表面是一个等势面 |
12.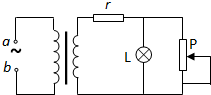 如图所示,理想变压器的副线圈连接灯泡L,输电线的等效电阻为r,a、b两端接在有效值恒定的正弦交流电源上,当滑动变阻器的滑片P向上移动时,以下说法中正确的是( )
如图所示,理想变压器的副线圈连接灯泡L,输电线的等效电阻为r,a、b两端接在有效值恒定的正弦交流电源上,当滑动变阻器的滑片P向上移动时,以下说法中正确的是( )
 如图所示,理想变压器的副线圈连接灯泡L,输电线的等效电阻为r,a、b两端接在有效值恒定的正弦交流电源上,当滑动变阻器的滑片P向上移动时,以下说法中正确的是( )
如图所示,理想变压器的副线圈连接灯泡L,输电线的等效电阻为r,a、b两端接在有效值恒定的正弦交流电源上,当滑动变阻器的滑片P向上移动时,以下说法中正确的是( )| A. | 副线圈中电流的频率减小 | B. | L变亮 | ||
| C. | r两端的电压增大 | D. | 原线圈输入功率增大 |
 如图所示,水平地面上固定一个光滑轨道ABC,该轨道由两个半径均为R的$\frac{1}{4}$圆弧$\widehat{AB}$、$\widehat{BC}$平滑连接而成,O1、O2分别为两段圆弧所对应的圆心,O1O2的连线竖直,O1D是一倾角为45°的虚线,现将一质量为m的小球(可视为质点)由轨道上P点(图中未标出)静止释放,重力加速度为g,求
如图所示,水平地面上固定一个光滑轨道ABC,该轨道由两个半径均为R的$\frac{1}{4}$圆弧$\widehat{AB}$、$\widehat{BC}$平滑连接而成,O1、O2分别为两段圆弧所对应的圆心,O1O2的连线竖直,O1D是一倾角为45°的虚线,现将一质量为m的小球(可视为质点)由轨道上P点(图中未标出)静止释放,重力加速度为g,求