��Ŀ����
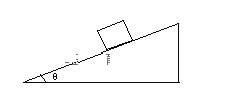
����Ŀ����ͼ��ʾ��AB��CDΪ����ͬ�İ��Ļ��湹�ɵķ����ͼ��ٵ糡�����Ʋ�ΪU��Բ��ΪO�����Ҳ���һ��ֱ��CD������O1�뾶ΪR��Բ������Բ��ΪO2��Բ��(��Բ����)���ڴ�ֱ��ֽ���������ǿ�ų���MN��һ���㹻����ƽ�壬��O1O2����ƽ�в�λ�����·�3R��������Ϊm�������Ϊq�Ĵ��������ӣ���ABԲ����Ӿ�ֹ��ʼ���ٵ�CD��O1�����ų�ƫת������MN�ϣ�������O1O2���߷�����ʱ�����Ӿ��ų�ƫת��ǡ�ô�Բ��O2�����·�G������ų�(����������Ӱ��)����
(1)�����ӵ���O1��ʱ�ٶȵĴ�С��Բ�δų��ĴŸ�Ӧǿ�ȴ�СB��
(2)��ͼ��P��(PO1��O1O2��30���н�)����������Q��(ͼ��δ����)�����ӣ���O1���˶����������õ�ʱ�䡣

���𰸡�(1) ![]() ��
��![]() ��(2)
��(2)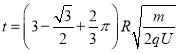
��������
(1)���������Ӵ�ABԲ���澲ֹ��ʼ���ٵ�CDԲ�����ϣ��ɶ��ܶ�����
![]()
���
![]()
��Բ�δų����������ṩ������
![]()
�������֪r=R�����ԴŸ�Ӧǿ��Ϊ
![]()
(2)��P�㱻���ٵ������˶��켣����ͼ��ʾ��
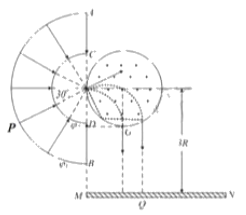
���ڴų��е��˶�����
![]()
�ڴų��е��˶�ʱ��
![]()
���ų���̽��������ʱ��
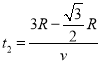
��O1�㵽̽���MN�����ʱ��
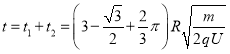

��ϰ��ϵ�д�
�����Ŀ