Question

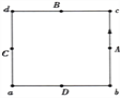
【题目】如图所示，有5个箭头代表船的划动方向（船头指向），其中C与河对岸垂直。每两个箭头之间的夹角为30°。已知水流速度v水=1 m/s，船在静水中的速度为v船=2 m/s。下列说法正确的是（ ）

A. 若船头指向为A，则船能到达出发点的正对岸

B. 若船头指向为B，则船能到达出发点的正对岸

C. 若船头指向为C，则船过河的时间最短

D. 若船头指向为D，则船过河的实际位移最大

Answer 1

【答案】BC

【解析】

AB.设静水速的方向偏向上游与河岸成θ，船能够到达出发点的正对岸时，根据平行四边形定则，v水=v船cosθ,得：θ=60.故A错误，B正确；

C. 船头指向为C，则船过河的时间最短为t=d/v.故C正确；

D. 船头与河岸之间的夹角越小，则船沿水流的方向的位移越大，船过河的实际位移越大。故船头指向为E，则船过河的实际位移最大。故D错误。

故选：BC.