题目内容
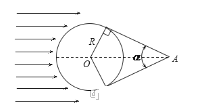
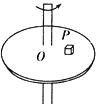
【题目】用一根细线一端系一小球(可视为质点),另一端固定在一光滑锥顶上,如图所示,设小球在水平面内绕图中虚线作匀速圆周运动的角速度为ω,线的张力为T,则T随ω2变化的图象是选项中的( )

A.  B.
B.  C.
C.  D.
D. 
【答案】C
【解析】设绳长为L,锥面与竖直方向夹角为θ,当ω=0时,小球静止,受重力mg、支持力N和绳的拉力T而平衡,T=mgcosθ≠0,故A B错误;ω增大时,T增大,N减小,当N=0时,角速度为ω0,当ω<ω0时,由牛顿第二定律得:Tsinθ-Ncosθ=mω2Lsinθ,Tcosθ+Nsinθ=mg,解得T=mω2Lsin2θ+mgcosθ;当ω>ω0时,小球离开锥子,绳与竖直方向夹角变大,设为β,由牛顿第二定律得Tsinβ=mω2Lsinβ,所以T=mLω2,可知T-ω2图线的斜率变大,故C正确,D错误。所以C正确,ABD错误。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目