题目内容
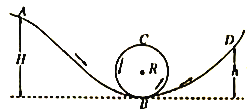
【题目】如图所示，一个小球(视为质点)从H=11m高处，由静止开始沿光滑弯曲轨道AB进入半径R=4m的竖直圆环内侧，且与圆环的动摩擦因数处处相等，当到达圆环顶点C时，刚好对轨道压力为零，然后沿CB圆弧滑下，进入光滑弧形轨道BD，到达高度为h的D点时速度为零，则h的值可能为
A. 10m B. 9.5m C. 9m D. 8.5m
【答案】B
【解析】
到达圆环顶点C时，刚好对轨道压力为零，则
可得C点的速度；由于从C到B过程克服摩擦力做功小于从B到C过程克服摩擦力的功，几何动能定理列出从C→B→D过程的方程即可求解h的范围。
到达圆环顶点C时，刚好对轨道压力为零，则，解得vC=2
m/s；则物体在BC阶段克服摩擦力做功为
，解得WBC=10m；由于从C到B过程小球对圆轨道的平均压力小于从B到C过程小球对圆轨道的平均压力，则从C到B过程克服摩擦力做功小于从B到C过程克服摩擦力的功，即0<WCB<10m；从C到D由动能定理：
，联立解得10m>h>9m；故选B.
练习册系列答案
相关题目
