题目内容
 如图所示,竖直放置的两块很大的平行金属板a、b,相距为d,ab间的电场强度为E,今有一带正电的微粒从a板下缘以初速度v0竖直向上射入电场,当它飞到b板时,速度大小不变,而方向变为水平方向,且刚好从高度也为d的狭缝穿过b板而进入bc区域,bc区域的宽度也为d,所加电场大小为E,方向竖直向上,磁感强度方向垂直纸面向里,磁场磁感应强度大小等于E/v0,重力加速度为g,则下列关于粒子运动的有关说法不正确的是( )
如图所示,竖直放置的两块很大的平行金属板a、b,相距为d,ab间的电场强度为E,今有一带正电的微粒从a板下缘以初速度v0竖直向上射入电场,当它飞到b板时,速度大小不变,而方向变为水平方向,且刚好从高度也为d的狭缝穿过b板而进入bc区域,bc区域的宽度也为d,所加电场大小为E,方向竖直向上,磁感强度方向垂直纸面向里,磁场磁感应强度大小等于E/v0,重力加速度为g,则下列关于粒子运动的有关说法不正确的是( )分析:将粒子在电场中的运动沿水平和竖直方向正交分解,水平分运动为初速度为零的匀加速运动,竖直分运动为末速度为零的匀减速运动,根据运动学公式和牛顿第二定律列式分析;粒子在复合场中运动时,由于电场力与重力平衡,故粒子做匀速圆周运动,洛伦兹力提供向心力.
解答:解:A、将粒子在电场中的运动沿水平和竖直方向正交分解,水平分运动为初速度为零的匀加速运动,竖直分运动为末速度为零的匀减速运动,根据运动学公式,有
水平方向:v0=at,d=
竖直方向:0=v0-gt
解得
a=g ①
t=
②
故A正确;
B、粒子在复合场中运动时,由于电场力与重力平衡,故粒子做匀速圆周运动,洛伦兹力提供向心力
qv0B=m
解得
r=
③
由①②③得到r=2d,故B正确;
C、由于r=2d,画出轨迹,如图
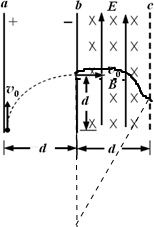
由几何关系,得到回旋角度为30°,故在复合场中的运动时间为
t2=
=
=
故C错误;
D、粒子在电场中运动时间为
t1=
=
=
故粒子在ab、bc区域中运动的总时间为t=t1+t2=
,故D正确;
本题选错误的,故选C.
水平方向:v0=at,d=
| ||
| 2g |
竖直方向:0=v0-gt
解得
a=g ①
t=
| v0 |
| g |
故A正确;
B、粒子在复合场中运动时,由于电场力与重力平衡,故粒子做匀速圆周运动,洛伦兹力提供向心力
qv0B=m
| v2 |
| r |
解得
r=
| mv0 |
| qB |
由①②③得到r=2d,故B正确;
C、由于r=2d,画出轨迹,如图

由几何关系,得到回旋角度为30°,故在复合场中的运动时间为
t2=
| T |
| 12 |
| πm |
| 6qB |
| πd |
| 3v0 |
故C错误;
D、粒子在电场中运动时间为
t1=
| d | ||
|
| d | ||
|
| 2d |
| v0 |
故粒子在ab、bc区域中运动的总时间为t=t1+t2=
| (π+6)d |
| 3v0 |
本题选错误的,故选C.
点评:本题关键是将粒子在电场中的运动正交分解为直线运动来研究,而粒子在复合场中运动时,重力和电场力平衡,洛仑兹力提供向心力,粒子做匀速圆周运动.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 如图所示,竖直放置的光滑圆环上套有一质量为m的小球,小球经过最高点时的速度为
如图所示,竖直放置的光滑圆环上套有一质量为m的小球,小球经过最高点时的速度为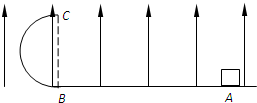 如图所示,竖直放置的半圆形绝缘轨道半径为R,下端与绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场E中.一质量为m、带电量为+q的物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好通过最高点C,场强大小
如图所示,竖直放置的半圆形绝缘轨道半径为R,下端与绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场E中.一质量为m、带电量为+q的物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好通过最高点C,场强大小 如图所示,竖直放置的轻弹簧一端固定在地面上,另一端与斜面体P固定,P与斜放的固定挡板MN接触且处于静止状态,则斜面体P此刻受到外力的个数可能是( )
如图所示,竖直放置的轻弹簧一端固定在地面上,另一端与斜面体P固定,P与斜放的固定挡板MN接触且处于静止状态,则斜面体P此刻受到外力的个数可能是( ) 物理选修3-3
物理选修3-3 如图所示,竖直放置的U形导轨宽为L,上端串有电阻R(其余导体部分的电阻都忽略不计).磁感应强度为B的匀强磁场方向垂直于纸面向外.金属棒ab的质量为m,与导轨接触良好,不计摩擦.从静止释放后ab保持水平而下滑.试求
如图所示,竖直放置的U形导轨宽为L,上端串有电阻R(其余导体部分的电阻都忽略不计).磁感应强度为B的匀强磁场方向垂直于纸面向外.金属棒ab的质量为m,与导轨接触良好,不计摩擦.从静止释放后ab保持水平而下滑.试求