题目内容
 如图甲所示,质量为m=1kg的物体置于倾角为θ=37°固定斜面上(斜面足够长),对物体施加平行于斜面向上的恒力F,作用时间t1=1s时撤去拉力,物体运动的部分v-t图象如图乙所示,取g=10m/s2.求:
如图甲所示,质量为m=1kg的物体置于倾角为θ=37°固定斜面上(斜面足够长),对物体施加平行于斜面向上的恒力F,作用时间t1=1s时撤去拉力,物体运动的部分v-t图象如图乙所示,取g=10m/s2.求:(1)物体与斜面间的动摩擦因数和拉力F的大小;
(2)t=6s时物体速度,并在乙图上将t=6s内物体运动的v-t图象补画完整,要求标明有关数据;
(3)物体返回出发点的速度大小.
分析:(1)根据图象可以求出匀加速直线运动和匀减速直线运动的加速度大小,根据牛顿第二定律列出匀加速运动和匀减速运动的力学方程,F-mgsinθ-μmgcosθ=ma1,mgsinθ+μmgcosθ=ma2,联立两方程求出动摩擦因数;
(2)先通过图象得到3s末速度为零,然后求出3s到6s物体的加速度,再根据速度时间关系公式求解6s末速度;
(3)先求解出前3s的位移,即上滑的位移;然后对下降过程运动位移时间关系公式列式求解下滑的时间.
(2)先通过图象得到3s末速度为零,然后求出3s到6s物体的加速度,再根据速度时间关系公式求解6s末速度;
(3)先求解出前3s的位移,即上滑的位移;然后对下降过程运动位移时间关系公式列式求解下滑的时间.
解答:解:(1)设力作用时物体的加速度为a1,对物体进行受力分析,
由牛顿第二定律有:F-mgsinθ-μmgcosθ=ma1
撤去力后,设物体的加速度为a2,
由牛顿第二定律有:mgsinθ+μmgcosθ=ma2
由图象可得a1=20m/s2; a2=10m/s2
代入解得F=30N; μ=0.5
故斜面与物体间的动摩擦因数为0.5,拉力大小为30N;
(2)3s末物体速度减为零,之后物体下滑做匀加速直线运动,
根据牛顿第二定律,有:mgsin37°-f=ma3
解得:a3=2m/s2
由速度时间公式,得到再过3s,有:v=a3t=6m/s
故物体6s末速度大小为6m/s.方向与初速度方向相反即沿斜面向下.
图象如下图所示.
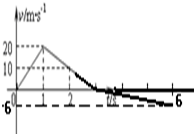
(3)速度时间图象与时间轴包围的面积表示位移,故:前3s的位移为:x=
×3×20=30m;
下降过程,根据位移时间关系公式,有:x=
a3t2,解得t=
=
s=
s;
故返回出发点的速度为:v3=a3t=2×
m/s=2
m/s≈11.0m/s;
答:(1)物体与斜面间的动摩擦因数为0.5,拉力F的大小为30N;
(2)t=6s时物体速度为6m/s,t=6s内物体运动的v-t图象如图所示;
(3)物体返回出发点的速度大小约为11.0m/s.
由牛顿第二定律有:F-mgsinθ-μmgcosθ=ma1
撤去力后,设物体的加速度为a2,
由牛顿第二定律有:mgsinθ+μmgcosθ=ma2
由图象可得a1=20m/s2; a2=10m/s2
代入解得F=30N; μ=0.5
故斜面与物体间的动摩擦因数为0.5,拉力大小为30N;
(2)3s末物体速度减为零,之后物体下滑做匀加速直线运动,
根据牛顿第二定律,有:mgsin37°-f=ma3
解得:a3=2m/s2
由速度时间公式,得到再过3s,有:v=a3t=6m/s
故物体6s末速度大小为6m/s.方向与初速度方向相反即沿斜面向下.
图象如下图所示.

(3)速度时间图象与时间轴包围的面积表示位移,故:前3s的位移为:x=
| 1 |
| 2 |
下降过程,根据位移时间关系公式,有:x=
| 1 |
| 2 |
|
|
| 30 |
故返回出发点的速度为:v3=a3t=2×
| 30 |
| 30 |
答:(1)物体与斜面间的动摩擦因数为0.5,拉力F的大小为30N;
(2)t=6s时物体速度为6m/s,t=6s内物体运动的v-t图象如图所示;
(3)物体返回出发点的速度大小约为11.0m/s.
点评:题关键受力分析后,根据牛顿第二定律,运用正交分解法求解出各个运动过程的加速度,然后结合运动学公式列式求解.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
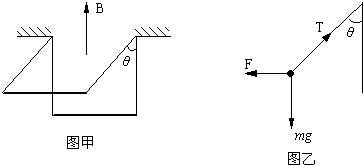
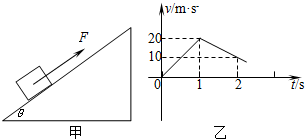 如图甲所示,质量为m=1kg的物体置于倾角为θ=37°的固定且足够长的斜面上,对物体施以平行于斜面向上的拉力F,t1=1s时撤去拉力,物体运动的部分v-t图象如图乙所示.试求:
如图甲所示,质量为m=1kg的物体置于倾角为θ=37°的固定且足够长的斜面上,对物体施以平行于斜面向上的拉力F,t1=1s时撤去拉力,物体运动的部分v-t图象如图乙所示.试求: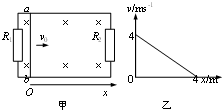 如图甲所示,质量为m=0.5kg、电阻r=1Ω的跨接杆ab可以无摩擦地沿水平固定导轨滑行,导轨足够长,两导轨间宽度为L=1m,导轨电阻不计,电阻R1=1.5Ω,R2=3Ω,装置处于竖直向下的匀强磁场中,磁感应强度为B=1T.杆从x轴原点O以水平初速度向右滑行,直到停止.已知杆在整个运动过程中v随位移x变化的关系如图乙所示.求:
如图甲所示,质量为m=0.5kg、电阻r=1Ω的跨接杆ab可以无摩擦地沿水平固定导轨滑行,导轨足够长,两导轨间宽度为L=1m,导轨电阻不计,电阻R1=1.5Ω,R2=3Ω,装置处于竖直向下的匀强磁场中,磁感应强度为B=1T.杆从x轴原点O以水平初速度向右滑行,直到停止.已知杆在整个运动过程中v随位移x变化的关系如图乙所示.求: