题目内容
18. 如图所示,平直公路A点左边的路段为柏油路面,右边路段为水泥路面.某汽车以速度v0经过A点时紧急刹车,要滑行到B点才能停下,若该汽车以2v0的速度在柏油路面上向右行驶,突然发现B处有障碍物,已知该汽车与柏油路面的动摩擦因数为μ1,与水泥路面的动摩擦因数为μ2,重力加速度为g,下列说法正确的是( )
如图所示,平直公路A点左边的路段为柏油路面,右边路段为水泥路面.某汽车以速度v0经过A点时紧急刹车,要滑行到B点才能停下,若该汽车以2v0的速度在柏油路面上向右行驶,突然发现B处有障碍物,已知该汽车与柏油路面的动摩擦因数为μ1,与水泥路面的动摩擦因数为μ2,重力加速度为g,下列说法正确的是( )| A. | AB段的长度为$\frac{{v}_{0}^{2}}{{μ}_{2}g}$ | |
| B. | 若汽车刚好不撞上障碍物,则在A点的速度应为$\frac{{v}_{0}}{2}$ | |
| C. | 若汽车刚好不撞上障碍物,则开始刹车的位置距A点的距离为$\frac{{3v}_{0}^{2}}{2{μ}_{1}g}$ | |
| D. | 若汽车刚好不撞上障碍物,则刹车滑行的总时间为$\frac{({μ}_{1}+{μ}_{2}){v}_{0}}{2{μ}_{1}{μ}_{2}g}$ |
分析 根据牛顿第二定律分别求出汽车在柏油路面和水泥路面上滑行的加速度大小,结合速度位移公式求出AB的长度.汽车如果刚好不撞上障碍物B,在A点的速度应为v0,根据速度位移公式求出开始刹车的位置距离A点的距离.根据速度时间公式分别求出在柏油路面和水泥路面上滑行的时间,从而得出总时间.
解答 解:A、水泥路面上运动的加速度大小为a2,则:μ2mg=ma2,解得:a2=μ2g,由运动学公式可得:$-2{a}_{2}{x}_{2}=0{-v}_{0}^{2}$,解得AB段的距离${x}_{2}=\frac{{v}_{0}^{2}}{2{μ}_{2}g}$,故A错误;
BC、根据题意,汽车如果刚好不撞上障碍物B,在A点的速度应为v0,
根据μ1mg=ma1得,a1=μ1g,可知开始刹车时距离A点的距离为:$x=\frac{(2{v}_{0})^{2}{-v}_{0}^{2}}{2{a}_{1}}=\frac{{3v}_{0}^{2}}{2{μ}_{1}g}$,故B错误,C正确.
D、若汽车刚好不撞上障碍物,在柏油路上运动时间为:${t}_{1}=\frac{2{v}_{0}-{v}_{0}}{{μ}_{1}g}$,在水泥路面上运动的时间为:${t}_{2}=\frac{{v}_{0}}{{μ}_{2}g}$,则总时间为:t=${t}_{1}+{t}_{2}=\frac{({μ}_{1}+{μ}_{2}){v}_{0}}{{μ}_{1}{μ}_{2}g}$,故D错误.
故选:C.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,知道加速度是联系力学和运动学的桥梁,注意汽车如果刚好不撞上障碍物B,在A点的速度应为v0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.如图所示,用一水平力F将一木块压在竖直墙上并保持静止,则墙对木块的摩擦力方向( )
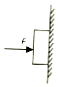

| A. | 竖直向上 | B. | 竖直向下 | C. | 水平向左 | D. | 水平向右 |
11.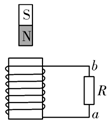 如图所示,螺线管与电阻R相连,磁铁从螺线管的正上方由静止释放,向下穿过螺线管,下列说法正确的是( )
如图所示,螺线管与电阻R相连,磁铁从螺线管的正上方由静止释放,向下穿过螺线管,下列说法正确的是( )
 如图所示,螺线管与电阻R相连,磁铁从螺线管的正上方由静止释放,向下穿过螺线管,下列说法正确的是( )
如图所示,螺线管与电阻R相连,磁铁从螺线管的正上方由静止释放,向下穿过螺线管,下列说法正确的是( )| A. | a的电势始终高于b的电势 | |
| B. | 通过电阻的电流先由a到b,后由b到a | |
| C. | 磁铁减少的重力势能等于回路产生的热量 | |
| D. | 磁铁刚离开螺线管时的加速度小于重力加速度 |
3.如图所示,物体静止在一固定在水平地面上的斜面上,下列说法正确的是( )


| A. | 物体对斜面的压力和斜面对物体的支持力是一对平衡力 | |
| B. | 物体所受重力和斜面对物体的作用力是一对平衡力 | |
| C. | 物体所受重力可以分解为沿斜面的力和对斜面的压力 | |
| D. | 物体对斜面的摩擦力和物体重力沿斜面的分力是一对作用力和反作用力 |
7.下列关于电场和磁场说法不正确的是( )
| A. | 电荷在电场强度为零的地方,受到的电场力一定为零 | |
| B. | 电荷在某处不受电场力作用,则该处电场强度一定为零 | |
| C. | 一小段通电导线放在磁感强度为零的地方,受到的安培力一定为零 | |
| D. | 一小段通电导线在某处不受安培力作用,则该处的磁感应强度一定为零 |
 如图所示,棒AB的A端靠在竖直墙壁上,B端搁在水平地面上,棒长为2m,在棒的中点C处有一质量m=0.5kg的小物体被固定在棒上(小物块和C点均未画出),棒的两端可分别沿墙面和地面滑动.当棒的B端以v=3m/s的速度向左匀速滑动,棒与墙面的夹角θ为30°时,(g=10m/s2) 求:
如图所示,棒AB的A端靠在竖直墙壁上,B端搁在水平地面上,棒长为2m,在棒的中点C处有一质量m=0.5kg的小物体被固定在棒上(小物块和C点均未画出),棒的两端可分别沿墙面和地面滑动.当棒的B端以v=3m/s的速度向左匀速滑动,棒与墙面的夹角θ为30°时,(g=10m/s2) 求: