题目内容
6. 如图所示,棒AB的A端靠在竖直墙壁上,B端搁在水平地面上,棒长为2m,在棒的中点C处有一质量m=0.5kg的小物体被固定在棒上(小物块和C点均未画出),棒的两端可分别沿墙面和地面滑动.当棒的B端以v=3m/s的速度向左匀速滑动,棒与墙面的夹角θ为30°时,(g=10m/s2) 求:
如图所示,棒AB的A端靠在竖直墙壁上,B端搁在水平地面上,棒长为2m,在棒的中点C处有一质量m=0.5kg的小物体被固定在棒上(小物块和C点均未画出),棒的两端可分别沿墙面和地面滑动.当棒的B端以v=3m/s的速度向左匀速滑动,棒与墙面的夹角θ为30°时,(g=10m/s2) 求:(1)此时A端的速度VA
(2)此时C点的速度VC
(3)此时棒对C处小物体的作用力有多大?
分析 (1)由速度的合成与分解可以求出A点沿墙竖直向下的速度大小,要注意的是关联AB两点的速度是沿AB方向的分量是相等的.
(2)分析可知C点是以墙角为圆心,以棒长一半为半径r=1m做圆周运动(斜边的中线等于斜边的一半),再由速度的合成与分解从而求出C点的速度.
(3)由于求出了C点此该做圆周运动的速度,从而也求出了此刻的向心加速度,而向心加速是由重力和棒对C物体的作用合力的分量提供,所以求出向心加速度沿竖直方向的分量,再由牛顿第二定律求出棒对C物体的作用.
解答  解:(1)由运动的合成和分解可知B点此时沿棒方向速度分量为V1=Vsinθ
解:(1)由运动的合成和分解可知B点此时沿棒方向速度分量为V1=Vsinθ
由杆连接特点可知A点此时沿棒方向速度分量也为V1=Vsinθ
则A点此时速度$V{\;}_A=\frac{V_I}{cosθ}=Vtanθ=\frac{{\sqrt{3}}}{3}V=\sqrt{3}m/s$
方向沿竖直墙向下
(2)分析可知C点是以墙角为圆心,以棒长一半为半径r=1m做圆周运动,VC方向为该点的切线方
由杆连接特点可知C点此时沿棒方向速度分量也为V1=Vsinθ
(或因为B点始终是匀速运动,则C点水平方向分速度始终也为V/2)则可得$V{\;}_C=\frac{Vsinθ}{cosθ}=\sqrt{3}m/s$
(3 )由于物块随C做圆周运动,则其此时的向心加速度为an
且${a_n}=\frac{{{V_C}^2}}{r}=3m/{s^2}$
而m在水平方向一直是匀速运动,m水平方向不受棒的作用力,则棒给m的作用力一定是沿竖直方向,
这个力F和物块的重力的合力使m的加速度一定是沿竖直方向,则$a=\frac{a_n}{cosθ}=2\sqrt{3}m/{s^2}$
由牛顿第二定律:F+mg=ma
解得F=-(5-$\sqrt{3}$)N=-3.27N
则此时棒对C处小物体的作用力大小为3.27N,方向竖直向上.
答:(1)此时A端的速度VA为$\sqrt{3}$m/s.
(2)此时C点的速度VC为$\sqrt{3}$ m/s.
(3)此时棒对C处小物体的作用力大小为3.27N,方向竖直向上.
点评 本题的靓点在于:①当杆沿墙下滑时,A、B两点速度是通过沿杆的分量联系起来的,由速度的合成就能求出A点下滑的速度.②令人费解的是C点的运动是圆周运动,由于C点到墙角的距离不变,则C点绕墙角做圆周运动.③此该C点速度由同上的方向可以求出,则向心加速度能求出,从而也求出沿竖直方向的分量,在此方向上应用牛顿第二定律就能求出棒对C物体的作用力.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图所示,卫星P绕地球做匀速圆周运动,卫星轨道平面与地球赤道平面在同一平面内,地球相对卫星P的张角为θ,若3颗卫星P在同一轨道适当位置,信号可以覆盖地球的全部赤道表面,下列说法正确的是( )
如图所示,卫星P绕地球做匀速圆周运动,卫星轨道平面与地球赤道平面在同一平面内,地球相对卫星P的张角为θ,若3颗卫星P在同一轨道适当位置,信号可以覆盖地球的全部赤道表面,下列说法正确的是( )| A. | 张角θ>60° | |
| B. | 张角θ越大,卫星运行的线速度越大 | |
| C. | 张角θ越大,每颗卫星的信号覆盖地球的表面积越大 | |
| D. | 若地球半径为R,则卫星离地面的高度为R($\frac{1}{sin\frac{θ}{2}}$-1) |
 如图所示,一辆货车利用跨过光滑定滑轮的轻质缆绳提升一箱货物,已知货箱的质量为M,货物的质量为m,货车以速度v向左做匀速直线运动,重力加速度为g,则下列说法正确的是( )
如图所示,一辆货车利用跨过光滑定滑轮的轻质缆绳提升一箱货物,已知货箱的质量为M,货物的质量为m,货车以速度v向左做匀速直线运动,重力加速度为g,则下列说法正确的是( )| A. | 到达图示位置时,货箱向上运动的速度大于$\frac{v}{cosθ}$ | |
| B. | 到达图示位置时,货箱向上运动的速度等于vcosθ | |
| C. | 运动过程中,M受到绳的拉力等于Mg | |
| D. | 运动过程中,M受到绳的拉力大于Mg |
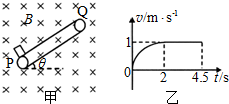 如图甲,一绝缘带电物块(视为质点)无初速度地放在皮带轮底端,皮带轮以恒定大小的速率沿顺时针方向转动,该装置处于垂直纸面向里的匀强磁场中,物块由底端P运动至皮带轮顶端Q的过程中,其v-t图象如图乙所示,物块全程运动的时间为4.5s且运动过程中电量保持不变,关于带电物块及运动过程的说法正确的是( )
如图甲,一绝缘带电物块(视为质点)无初速度地放在皮带轮底端,皮带轮以恒定大小的速率沿顺时针方向转动,该装置处于垂直纸面向里的匀强磁场中,物块由底端P运动至皮带轮顶端Q的过程中,其v-t图象如图乙所示,物块全程运动的时间为4.5s且运动过程中电量保持不变,关于带电物块及运动过程的说法正确的是( )| A. | 该物块带正电 | |
| B. | 皮带轮的传动速度大小一定为l m/s | |
| C. | 若已知皮带的长度,可求出该过程中物块与皮带发生的相对位移 | |
| D. | 在2s~4.5s内,物块与皮带仍可能有相对运动 |
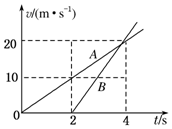 A、B两物体从同一点开始运动,由A、B两物体的速度-时间图象(如图)可知下述说法中正确的是( )
A、B两物体从同一点开始运动,由A、B两物体的速度-时间图象(如图)可知下述说法中正确的是( )| A. | A、B两物体同时从同一位置向同一方向运动 | |
| B. | A、B两物体自同一时刻向不同方向运动 | |
| C. | A、B两物体的加速度大小均为5 m/s2 | |
| D. | A、B两物体在A出发后4 s时,相距20 m |
 如图所示,平直公路A点左边的路段为柏油路面,右边路段为水泥路面.某汽车以速度v0经过A点时紧急刹车,要滑行到B点才能停下,若该汽车以2v0的速度在柏油路面上向右行驶,突然发现B处有障碍物,已知该汽车与柏油路面的动摩擦因数为μ1,与水泥路面的动摩擦因数为μ2,重力加速度为g,下列说法正确的是( )
如图所示,平直公路A点左边的路段为柏油路面,右边路段为水泥路面.某汽车以速度v0经过A点时紧急刹车,要滑行到B点才能停下,若该汽车以2v0的速度在柏油路面上向右行驶,突然发现B处有障碍物,已知该汽车与柏油路面的动摩擦因数为μ1,与水泥路面的动摩擦因数为μ2,重力加速度为g,下列说法正确的是( )| A. | AB段的长度为$\frac{{v}_{0}^{2}}{{μ}_{2}g}$ | |
| B. | 若汽车刚好不撞上障碍物,则在A点的速度应为$\frac{{v}_{0}}{2}$ | |
| C. | 若汽车刚好不撞上障碍物,则开始刹车的位置距A点的距离为$\frac{{3v}_{0}^{2}}{2{μ}_{1}g}$ | |
| D. | 若汽车刚好不撞上障碍物,则刹车滑行的总时间为$\frac{({μ}_{1}+{μ}_{2}){v}_{0}}{2{μ}_{1}{μ}_{2}g}$ |
| A. | 做曲线运动的物体,合外力一定为零 | |
| B. | 做曲线运动的物体,合外力一定是变化的 | |
| C. | 做曲线运动的物体,合外力方向与速度方向不在同一直线上 | |
| D. | 做曲线运动的物体,合外力方向与速度方向在同一直线上 |