题目内容
18.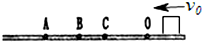 如图所示,在水平面上有一个小物块质量为m,从O点右侧给它一个初速度沿水平面做匀减速直线运动,依次经过O、C、B、A四点,最终停在A点,A、B、C三点到O点的距离分别为L1、L2、L3,由A、B、C到O点所用时间分别为t1、t2、t3;下列结论正确的是( )
如图所示,在水平面上有一个小物块质量为m,从O点右侧给它一个初速度沿水平面做匀减速直线运动,依次经过O、C、B、A四点,最终停在A点,A、B、C三点到O点的距离分别为L1、L2、L3,由A、B、C到O点所用时间分别为t1、t2、t3;下列结论正确的是( )| A. | $\frac{L_2}{t_2}=\frac{v_0}{2}$ | B. | $\frac{L_2}{{{t_2}^2}}>\frac{L_3}{{{t_3}^2}}$ | ||
| C. | $\frac{L_1}{t_1}<\frac{v_0}{2}$ | D. | $\frac{L_1}{{{t_1}^2}}<\frac{L_2}{{{t_2}^2}}$ |
分析 由于物体做匀减速运动,由O到C、B、A做匀减速运动,故平均速度逐渐减小,由逆向转换法知由O点向C点、B点、A点做初速度为零的匀加速直线运动,有位移时间关系判定即可.
解答 解:AC、由于物体做匀减速运动,由O到C、B、A做匀减速运动,故平均速度逐渐减小,故有$\frac{v_0}{2}>\frac{L_1}{t_1}>\frac{L_2}{t_2}>\frac{L_3}{t_3}$,A错误、C正确;
BD、由逆向转换法知由A点向B点、C点、O点做初速度为零的匀加速直线运动,
有$\frac{1}{2}a{t^2}_1={L_1}$,$\frac{1}{2}a{t^2}_2={L_2}$,$\frac{1}{2}a{t^2}_3={L_3}$,可得$\frac{L_1}{{{t^2}_1}}$=$\frac{L_2}{{{t^2}_2}}$=$\frac{L_3}{{{t^2}_3}}$=$\frac{1}{2}a$,B错误,D错误;
故选:C
点评 此题考察匀变速直线运动规律的应用,注意末速度为零的匀减速直线运动可以逆向视为初速度为零的匀加速直线运动,这样计算可以使问题简单化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.小船匀速逆流而上,经过桥下时箱子落水了,船继续前进一段时间后才发现,并立即调头以相同的静水船速顺流而下,经过1h在下游距桥7.2km处追上.则河水流动速度为( )
| A. | 7.2km/h | B. | 3.6km/h | ||
| C. | 10m/s | D. | 条件不足,无法确定 |
3.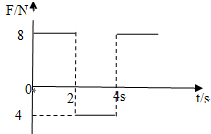 一质点(m=2kg)正自东向西在光滑水平面上做匀速直线运动,速度大小为4m/s,从某时刻起受到一个沿东西方向的力作用,如图,是该力随时间周期性的变化图象(从该时刻开始计时,规定向东方向为正方向)下列说法正确的是( )
一质点(m=2kg)正自东向西在光滑水平面上做匀速直线运动,速度大小为4m/s,从某时刻起受到一个沿东西方向的力作用,如图,是该力随时间周期性的变化图象(从该时刻开始计时,规定向东方向为正方向)下列说法正确的是( )
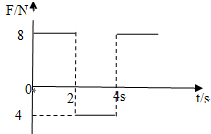 一质点(m=2kg)正自东向西在光滑水平面上做匀速直线运动,速度大小为4m/s,从某时刻起受到一个沿东西方向的力作用,如图,是该力随时间周期性的变化图象(从该时刻开始计时,规定向东方向为正方向)下列说法正确的是( )
一质点(m=2kg)正自东向西在光滑水平面上做匀速直线运动,速度大小为4m/s,从某时刻起受到一个沿东西方向的力作用,如图,是该力随时间周期性的变化图象(从该时刻开始计时,规定向东方向为正方向)下列说法正确的是( )| A. | 2s末物块的速度大小为4m/s | B. | 从该时刻起,质点做往复运动 | ||
| C. | 8s末质点的速度大小为12m/s | D. | 8s末质点的速度大小为4m/s |
10.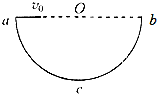 如图所示,ab为竖直平面内的半圆环acb的水平直径,c为环上最低点,环半径为R.将一个小球从a点以初速度v0沿ab方向抛出,设重力加速度为g,不计空气阻力.( )
如图所示,ab为竖直平面内的半圆环acb的水平直径,c为环上最低点,环半径为R.将一个小球从a点以初速度v0沿ab方向抛出,设重力加速度为g,不计空气阻力.( )
 如图所示,ab为竖直平面内的半圆环acb的水平直径,c为环上最低点,环半径为R.将一个小球从a点以初速度v0沿ab方向抛出,设重力加速度为g,不计空气阻力.( )
如图所示,ab为竖直平面内的半圆环acb的水平直径,c为环上最低点,环半径为R.将一个小球从a点以初速度v0沿ab方向抛出,设重力加速度为g,不计空气阻力.( )| A. | v0越大,小球落在圆环时的时间越长 | |
| B. | 当小球的初速度v0<$\frac{{\sqrt{2gR}}}{2}$时,将撞击到环上的圆弧ac段 | |
| C. | 无论v0取何值,小球都不可能垂直撞击圆环 | |
| D. | 当v0取适当值,小球可以垂直撞击圆环 |
7.下列属于离心现象的是( )
| A. | 投篮球 | B. | 洗衣机脱水 | ||
| C. | 汽车高速转弯容易甩出车道 | D. | 旋转雨伞甩掉雨伞上的水 |