题目内容
3.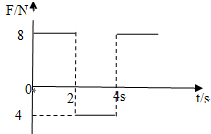 一质点(m=2kg)正自东向西在光滑水平面上做匀速直线运动,速度大小为4m/s,从某时刻起受到一个沿东西方向的力作用,如图,是该力随时间周期性的变化图象(从该时刻开始计时,规定向东方向为正方向)下列说法正确的是( )
一质点(m=2kg)正自东向西在光滑水平面上做匀速直线运动,速度大小为4m/s,从某时刻起受到一个沿东西方向的力作用,如图,是该力随时间周期性的变化图象(从该时刻开始计时,规定向东方向为正方向)下列说法正确的是( )| A. | 2s末物块的速度大小为4m/s | B. | 从该时刻起,质点做往复运动 | ||
| C. | 8s末质点的速度大小为12m/s | D. | 8s末质点的速度大小为4m/s |
分析 根据牛顿第二定律求出各段时间内的加速度,结合速度的变化量,求出各个时刻的速度大小.
解答 解:A、由牛顿第二运动定律可得在0~2s内,物体的加速度a1=$\frac{{F}_{1}}{m}=\frac{8}{2}m/{s}^{2}=4m/{s}^{2}$,物体速度变化量为△v1=a1△t1=4×2m/s=8m/s,故在t=2s的速度为v2=-4m/s+8m/s=4m/s,故A正确;
B、在2s~4s内,物体的加速度a2=$\frac{{F}_{2}}{m}=\frac{-4}{2}m/{s}^{2}=-2m/{s}^{2}$,物体速度变化量为△v2=a2△t2=-2×2m/s=-4m/s,物体在t=4s的速度为v4=4m/s-4m/s=0,在t=4s后继续向右匀加速直线运动,故B错误;
C、在4s~6s内,物体的加速度a3=$\frac{{F}_{3}}{m}=\frac{8}{2}m/{s}^{2}=4m/{s}^{2}$,物体速度变化量为△v3=a3△t3=4×2m/s=8m/s,在6s~8s内,物体的加速度a4=$\frac{{F}_{4}}{m}=\frac{-4}{2}m/{s}^{2}=-2m/{s}^{2}$,物体速度变化量为△v4=a4t4=-2×2m/s=-4m/s,故在t=8s末的速度为v8=△v3+△v4=4m/s,故C错误,D正确.
故选:AD.
点评 本题考查了牛顿第二定律和运动学公式的基本运用,关键理清物体的运动规律,结合牛顿第二定律和运动学公式综合求解.

练习册系列答案
相关题目
14. 物体A、B都静止在同一水平面上,它们的质量分别是mA和mB,与水平面之间的动摩擦因数分别为μA和μB.用平行于水平面的力F分别拉物体A、B,得到加速度a和拉力F的关系图象分别如图中A、B所示.已知tan26°34′=0.5,利用图象可求出A、B两物体与水平面之间的动摩擦因数μA和μB的数值分别为( )
物体A、B都静止在同一水平面上,它们的质量分别是mA和mB,与水平面之间的动摩擦因数分别为μA和μB.用平行于水平面的力F分别拉物体A、B,得到加速度a和拉力F的关系图象分别如图中A、B所示.已知tan26°34′=0.5,利用图象可求出A、B两物体与水平面之间的动摩擦因数μA和μB的数值分别为( )
 物体A、B都静止在同一水平面上,它们的质量分别是mA和mB,与水平面之间的动摩擦因数分别为μA和μB.用平行于水平面的力F分别拉物体A、B,得到加速度a和拉力F的关系图象分别如图中A、B所示.已知tan26°34′=0.5,利用图象可求出A、B两物体与水平面之间的动摩擦因数μA和μB的数值分别为( )
物体A、B都静止在同一水平面上,它们的质量分别是mA和mB,与水平面之间的动摩擦因数分别为μA和μB.用平行于水平面的力F分别拉物体A、B,得到加速度a和拉力F的关系图象分别如图中A、B所示.已知tan26°34′=0.5,利用图象可求出A、B两物体与水平面之间的动摩擦因数μA和μB的数值分别为( )| A. | μA=$\frac{1}{15}$,μB=$\frac{1}{30}$ | B. | μA=0.2,μB=0.1 | C. | μA=0.1,μB=0.05 | D. | μA=0.1,μB=0.2 |
11.有四个金属导体,它们的U-I图如图所示,电阻最大的导体是( )


| A. | a | B. | b | C. | c | D. | d |
18.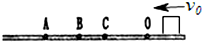 如图所示,在水平面上有一个小物块质量为m,从O点右侧给它一个初速度沿水平面做匀减速直线运动,依次经过O、C、B、A四点,最终停在A点,A、B、C三点到O点的距离分别为L1、L2、L3,由A、B、C到O点所用时间分别为t1、t2、t3;下列结论正确的是( )
如图所示,在水平面上有一个小物块质量为m,从O点右侧给它一个初速度沿水平面做匀减速直线运动,依次经过O、C、B、A四点,最终停在A点,A、B、C三点到O点的距离分别为L1、L2、L3,由A、B、C到O点所用时间分别为t1、t2、t3;下列结论正确的是( )
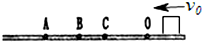 如图所示,在水平面上有一个小物块质量为m,从O点右侧给它一个初速度沿水平面做匀减速直线运动,依次经过O、C、B、A四点,最终停在A点,A、B、C三点到O点的距离分别为L1、L2、L3,由A、B、C到O点所用时间分别为t1、t2、t3;下列结论正确的是( )
如图所示,在水平面上有一个小物块质量为m,从O点右侧给它一个初速度沿水平面做匀减速直线运动,依次经过O、C、B、A四点,最终停在A点,A、B、C三点到O点的距离分别为L1、L2、L3,由A、B、C到O点所用时间分别为t1、t2、t3;下列结论正确的是( )| A. | $\frac{L_2}{t_2}=\frac{v_0}{2}$ | B. | $\frac{L_2}{{{t_2}^2}}>\frac{L_3}{{{t_3}^2}}$ | ||
| C. | $\frac{L_1}{t_1}<\frac{v_0}{2}$ | D. | $\frac{L_1}{{{t_1}^2}}<\frac{L_2}{{{t_2}^2}}$ |
15.对于重力的理解,下列说法正确的是( )
| A. | 重力和运动状态无关,可用公式G=mg计算 | |
| B. | 物体的重心一定在物体上 | |
| C. | 超重时重力最大,失重时重力最小 | |
| D. | 重力的方向永远是垂直向下的 |
 地面上有一个半径为R的圆形跑道,高为h的平台边缘上的P点在地面上P′点的正上方,P′与跑道圆心O的距离为L(L>R),如图所示.跑道上停有一辆小车,现从P点水平抛出小沙袋,使其落入小车中(沙袋所受空气阻力不计).问:
地面上有一个半径为R的圆形跑道,高为h的平台边缘上的P点在地面上P′点的正上方,P′与跑道圆心O的距离为L(L>R),如图所示.跑道上停有一辆小车,现从P点水平抛出小沙袋,使其落入小车中(沙袋所受空气阻力不计).问:
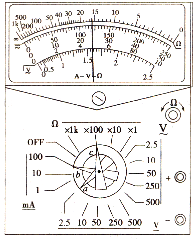 在正确操作的情况下,多用电表的指针指在图示位置.
在正确操作的情况下,多用电表的指针指在图示位置.