题目内容
 如图所示,在平面直角坐标系xOy的第II、III象限内存在沿y轴负方向的匀强电场,场强E=50V/m;一圆心在O1点,半径R=5cm的绝缘弹性圆筒在与y轴切点O处开有小孔a,筒内有垂直纸面向里的匀强磁场.现从P(-10cm,-5cm)处沿与x轴正向成45°方向发射比荷q/m=2×103C/kg的带正电粒子,粒子都恰能通过原点O沿x轴正向射出电场并进入磁场.不计粒子重力,试求:
如图所示,在平面直角坐标系xOy的第II、III象限内存在沿y轴负方向的匀强电场,场强E=50V/m;一圆心在O1点,半径R=5cm的绝缘弹性圆筒在与y轴切点O处开有小孔a,筒内有垂直纸面向里的匀强磁场.现从P(-10cm,-5cm)处沿与x轴正向成45°方向发射比荷q/m=2×103C/kg的带正电粒子,粒子都恰能通过原点O沿x轴正向射出电场并进入磁场.不计粒子重力,试求:(1)粒子在P点的发射速度v;
(2)若粒子进入圆筒后与圆筒发生四次碰撞后又恰从孔a射出磁场,已知该带电粒子每次与圆筒发生碰撞时电量和能量都不损失,求磁感应强度B的大小.(可用三角函数表示)
分析:(1)粒子从P点斜向上到达O点的过程做匀变速的曲线运动,它的逆过程可以看做是从O到P的类平抛运动,所以平抛运动的规律即可求得粒子的发射速度.
(2)带电粒子进入磁场中作匀速圆周运动,由洛伦兹力提供向心力.由题,带电粒子每次与筒壁发生碰撞时电量和能量都不损失,每次碰撞前后粒子速度大小不变、速度方向总是沿着圆筒半径方向,粒子与圆筒壁4个碰撞点与小孔a恰好将圆筒壁五等分,根据对称性,由几何知识求出轨迹圆弧对应的圆心角,即可求出轨迹半径,由牛顿第二定律求出磁感应强度B.
(2)带电粒子进入磁场中作匀速圆周运动,由洛伦兹力提供向心力.由题,带电粒子每次与筒壁发生碰撞时电量和能量都不损失,每次碰撞前后粒子速度大小不变、速度方向总是沿着圆筒半径方向,粒子与圆筒壁4个碰撞点与小孔a恰好将圆筒壁五等分,根据对称性,由几何知识求出轨迹圆弧对应的圆心角,即可求出轨迹半径,由牛顿第二定律求出磁感应强度B.
解答:解:(1)粒子在电场中运动的加速度:a=
=
?E=1×105m/s2
粒子在O点时的速度为v0,则由平抛运动的规律可得:L=v0t=10cm
y=
at2=5cm
代入数据解得:v0=100m/s
粒子在P点的速度:v=
v0=100
m/s
(2)带电粒子在磁场中作匀速圆周运动,qvB=m
…①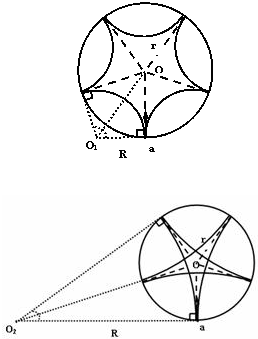
得:B=
…②
由于带电粒子与圆筒壁碰撞时无电量和能量损失,那么每次碰撞前后粒子速度大小不变、速度方向总是沿着圆筒半径方向,4个碰撞点与小孔a恰好将圆筒壁五等分,粒子在圆筒内的轨迹具有对称性,由5段相同的圆弧组成,设每段轨迹圆弧对应的圆心角为θ,则由几何关系可得:
=tan
解得,R=
…③
有两种情形符合题意(如图所示):
Ⅰ情形1:每段轨迹圆弧对应的圆心角为:
θ=π-
=
联立②③并代入θ值得:B=
?
…④
将数据代入④式得:B1=cot
T…⑤
Ⅱ情形2:每段轨迹圆弧对应的圆心角为:θ=π-
=
联立②③并代入θ值及数据得:B2=cot
T
答:(1)粒子在P点的发射速度为100
m/s;
(2)若粒子进入圆筒后与圆筒发生四次碰撞后又恰从孔a射出磁场,磁感应强度B的大小为B1=cot
T或B2=cot
T.
| qE |
| m |
| q |
| m |
粒子在O点时的速度为v0,则由平抛运动的规律可得:L=v0t=10cm
y=
| 1 |
| 2 |
代入数据解得:v0=100m/s
粒子在P点的速度:v=
| 2 |
| 2 |
(2)带电粒子在磁场中作匀速圆周运动,qvB=m
| ||
| r |

得:B=
| mv0 |
| qr |
由于带电粒子与圆筒壁碰撞时无电量和能量损失,那么每次碰撞前后粒子速度大小不变、速度方向总是沿着圆筒半径方向,4个碰撞点与小孔a恰好将圆筒壁五等分,粒子在圆筒内的轨迹具有对称性,由5段相同的圆弧组成,设每段轨迹圆弧对应的圆心角为θ,则由几何关系可得:
| r |
| R |
| θ |
| 2 |
解得,R=
| r | ||
tan
|
有两种情形符合题意(如图所示):
Ⅰ情形1:每段轨迹圆弧对应的圆心角为:
θ=π-
| 2π |
| 5 |
| 3π |
| 5 |
联立②③并代入θ值得:B=
tan
| ||
| r |
| mv0 |
| q |
将数据代入④式得:B1=cot
| π |
| 5 |
Ⅱ情形2:每段轨迹圆弧对应的圆心角为:θ=π-
| 4π |
| 5 |
| π |
| 5 |
联立②③并代入θ值及数据得:B2=cot
| 2π |
| 5 |
答:(1)粒子在P点的发射速度为100
| 2 |
(2)若粒子进入圆筒后与圆筒发生四次碰撞后又恰从孔a射出磁场,磁感应强度B的大小为B1=cot
| π |
| 5 |
| 2π |
| 5 |
点评:本题的解题关键是抓住对称性,由几何知识得到粒子的轨迹半径与圆筒半径的关系,画出粒子运动的轨迹是分析的基础.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
 如图所示,在平面直角坐标系xOy的第一象限内,有垂直纸面向里的匀强磁场,磁感应强度为B=2T.一对电子和正电子从O点沿纸面以相同的速度v射入磁场中,速度方向与磁场边界0x成30.角,求:电子和止电子在磁场中运动的时间为多少?
如图所示,在平面直角坐标系xOy的第一象限内,有垂直纸面向里的匀强磁场,磁感应强度为B=2T.一对电子和正电子从O点沿纸面以相同的速度v射入磁场中,速度方向与磁场边界0x成30.角,求:电子和止电子在磁场中运动的时间为多少?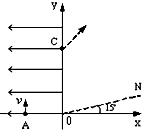 如图所示,在平面直角坐标系xoy中的第一象限内存在磁感应强度大小为B、方向垂直于坐标平面向内的有界圆形匀强磁场区域(图中未画出);在第二象限内存在沿x轴负方向的匀强电场.一粒子源固定在x轴上的A点,A点坐标为(-L,0).粒子源沿Y轴正方向释放出速度大小为v的电子,电子恰好能通过y轴上的C点,C点坐标为(0,2L),电子经过磁场后恰好垂直通过第一象限内与x轴正方向成15°角的射线ON(已知电子的质量为m,电荷量为e,不考虑粒子的重力和粒子之间的相互作用).求:
如图所示,在平面直角坐标系xoy中的第一象限内存在磁感应强度大小为B、方向垂直于坐标平面向内的有界圆形匀强磁场区域(图中未画出);在第二象限内存在沿x轴负方向的匀强电场.一粒子源固定在x轴上的A点,A点坐标为(-L,0).粒子源沿Y轴正方向释放出速度大小为v的电子,电子恰好能通过y轴上的C点,C点坐标为(0,2L),电子经过磁场后恰好垂直通过第一象限内与x轴正方向成15°角的射线ON(已知电子的质量为m,电荷量为e,不考虑粒子的重力和粒子之间的相互作用).求: 如图所示,在平面直角坐标系xoy的0≤x≤2L、0≤y≤L区域内存在沿y轴正向的匀强电场,一质量为m,电荷量为q,不计重力,带正电的粒子以速度v0从坐标原点O沿x轴正向射入电场后,恰好从M(2L,L)点离开电场,粒子离开电场后将有机会进入一个磁感应强度大小为
如图所示,在平面直角坐标系xoy的0≤x≤2L、0≤y≤L区域内存在沿y轴正向的匀强电场,一质量为m,电荷量为q,不计重力,带正电的粒子以速度v0从坐标原点O沿x轴正向射入电场后,恰好从M(2L,L)点离开电场,粒子离开电场后将有机会进入一个磁感应强度大小为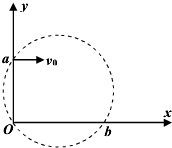 如图所示,在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场,其边界过原点O和y轴上的点a(0,L)一质量为m、电荷量为e的电子从a点以初速度v0平行于x轴正方向射入磁场,并从x轴上的b点射出磁场,此时速度方向与x轴正方向的夹角为60°.下列说法中正确的是( )
如图所示,在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场,其边界过原点O和y轴上的点a(0,L)一质量为m、电荷量为e的电子从a点以初速度v0平行于x轴正方向射入磁场,并从x轴上的b点射出磁场,此时速度方向与x轴正方向的夹角为60°.下列说法中正确的是( )