题目内容
我国成功发射一颗绕月运行的探月卫星.设该卫星的轨道是圆形的,且贴近月球表面.已知月球的质量约为地球质量的
,月球的半径约为地球半径的
,地球上的第一宇宙速度为v1,地球表面重力加速度为g.求:
(1)月球表面的重力加速度;
(2)该探月卫星绕月运行的速率.
| 1 |
| 81 |
| 1 |
| 4 |
(1)月球表面的重力加速度;
(2)该探月卫星绕月运行的速率.
分析:(1)根据万有引力等于重力得出表面重力加速度与中心天体半径和质量的关系,从而通过地球表面的重力加速度求出月球表面的重力加速度.
(2)根据万有引力提供向心力,求出速度与轨道半径的关系,从而得出探月卫星的速度与地球第一宇宙速度的关系.
(2)根据万有引力提供向心力,求出速度与轨道半径的关系,从而得出探月卫星的速度与地球第一宇宙速度的关系.
解答:解:(1)根据万有引力等于重力得,G
=mg
g=
则
=
=
=
所以g月=
g.
(2)根据万有引力提供向心力得
G
=m
解得v=
所以
=
=
.
则v=
v1.
答:(1)月球表面的重力加速度为g月=
g.
(2)探月卫星绕月运行的速率为v=
v1.
| Mm |
| R2 |
g=
| GM |
| R2 |
则
| g月 |
| g地 |
| ||
|
| ||
|
| 16 |
| 81 |
所以g月=
| 16 |
| 81 |
(2)根据万有引力提供向心力得
G
| Mm |
| R2 |
| v2 |
| R |
解得v=
|
所以
| v |
| v1 |
|
| 2 |
| 9 |
则v=
| 2 |
| 9 |
答:(1)月球表面的重力加速度为g月=
| 16 |
| 81 |
(2)探月卫星绕月运行的速率为v=
| 2 |
| 9 |
点评:解决本题的关键掌握万有引力等于重力和万有引力提供向心力这两个理论,并能熟练运用.

练习册系列答案
相关题目
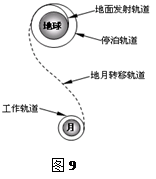
 2007年10月24日18时零5分,我国成功发射一颗探月卫星“嫦娥一号”.探月卫星绕地经过3次变轨飞行180多万公里,于2007年11月5日成功进入月球捕获轨道,如图I轨道;11月6日经第2次变轨进入环月轨道,如图II轨道;11月7日经第3次变轨进入工作轨道,如图9-III轨道.经过测试调整于2007年11月20日向地球发回首张照片,“嫦娥一号”成功发射在我国又掀起了新一轮航天热.关于“嫦娥一号”探月卫星,下列说法正确的是( )
2007年10月24日18时零5分,我国成功发射一颗探月卫星“嫦娥一号”.探月卫星绕地经过3次变轨飞行180多万公里,于2007年11月5日成功进入月球捕获轨道,如图I轨道;11月6日经第2次变轨进入环月轨道,如图II轨道;11月7日经第3次变轨进入工作轨道,如图9-III轨道.经过测试调整于2007年11月20日向地球发回首张照片,“嫦娥一号”成功发射在我国又掀起了新一轮航天热.关于“嫦娥一号”探月卫星,下列说法正确的是( )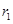 和
和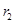 ,地球半径为
,地球半径为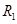 ,月球半径为
,月球半径为 ,地球表面重力加速度为g,月球表面重力加速度为
,地球表面重力加速度为g,月球表面重力加速度为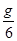 .求:
.求: