��Ŀ����
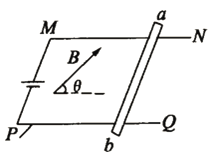
����Ŀ����ͼ��������K������ȵ��ӣ������ͳ��ٶȾ����ƣ�ͨ�����ٵ糡����ͼʾ���ߴ�ֱ������ǿ�ų������ų������㹻��������ΪL��2.5cm����֪���ٵ�ѹΪU��182V���Ÿ�Ӧǿ��B��9.1��10-4T�����ӵĵ���![]() ����������
����������![]() ����
����

��1)�����ڴų����˶����ٶȴ�Сv�Ͱ뾶R��
(2)�����ڴų����˶���ʱ��t(�������![]() )��
)��
(3)�����ٵ�ѹ��С���Ըı䣬�����������䣬Ϊʹ�����ڴų��е��˶�ʱ��������ٵ�ѹUӦ����ʲô������
���𰸡�(1)![]() ,0.05m��2��
,0.05m��2��![]() ��3��
��3��![]()
��������
Ӧ�ö��ܶ������ӽ�����Ӵ����糡ʱ���ٶ������ӽ���ų�����ƫת��������Բ���˶��������������ṩ������������ţ�ٵڶ���������ڴų��е��˶��뾶R���ȸ���Բ���˶���֪ʶ��õ����ڴų����˶�������T�������켣���ɼ���֪ʶ��������ڴų����˶��켣����Ӧ��Բ�Ľ�������![]() ����ڴų����˶���ʱ��t��Ϊʹ�����ڴų��е��˶�ʱ��������ӹ켣��Ӧ��Բ�ĽDZ���������Բ�Ľ�Ϊ180�����켣ǡ����ų��ұ߽����У���ù켣�뾶����������Ľ�����������
����ڴų����˶���ʱ��t��Ϊʹ�����ڴų��е��˶�ʱ��������ӹ켣��Ӧ��Բ�ĽDZ���������Բ�Ľ�Ϊ180�����켣ǡ����ų��ұ߽����У���ù켣�뾶����������Ľ�����������
�⣺��1�����ٵ糡�ж��ܶ�����
![]()
���![]()
�����ڴų���Բ���˶�����ţ�ٵڶ�����![]()
���![]()
��2���ų����˶�������![]()
�ɼ��ι�ϵ![]()
��![]()
![]()
��3�������ڴų��е��˶�ʱ���ʱ��Բ�Ľ�Ϊ![]()
���˶��켣��ų��ҽ�����ʱ��![]()
������![]()
�� ![]() ��
��![]()
���![]()
����![]()