题目内容
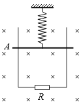
【题目】如图,两根足够长的光滑金属导轨竖直放置,底端接电阻R,轻弹簧上端固定,下端悬挂质量为m的金属棒,金属棒和导轨接触良好。除电阻R外,其余电阻不计。导轨处于匀强磁场中,磁场方向垂直导轨所在平面。静止时金属棒位于A处,此时弹簧的伸长量为Δl,弹性势能为Ep。重力加速度大小为g。将金属棒从弹簧原长位置由静止释放,金属棒在运动过程中始终保持水平,则
A. 当金属棒的速度最大时,弹簧的伸长量为Δl
B. 电阻R上产生的总热量等于mgΔl-Ep
C. 金属棒第一次到达A处时,其加速度方向向下
D. 金属棒第一次下降过程通过电阻R的电荷量比第一次上升过程的多
【答案】BD
【解析】
A、金属棒的速度最大时,合力为零,由平衡条件有 mg=kx+F安.金属棒原来静止时有 mg=k△l.两式对比可得 x<△l,即金属棒的速度最大时,弹簧的伸长量小于△l.故A错误。
B、金属棒最后静止在A处,从释放到金属棒最后静止的过程中,其重力势能减小,转化成内能和弹簧的弹性势能,则由能量守恒定律可得:电阻R上产生的热量 Q=mg△l﹣Ep.故B正确。
C、金属棒第一次到达A处时,受到重力、弹簧的弹力和安培力,且重力与弹力大小相等、方向相反,安培力方向向上,所以合力等于安培力,方向向上,可知加速度方向向上,故C错误。
D、根据能量守恒定律知,金属棒第一次下降的高度大于第一次上升的高度,根据q![]() 分析知,金属棒第一次下降过程磁通量的变化比第一次上升过程磁通量的变化量大,则金属棒第一次下降过程通过电阻R的电荷量比第一次上升过程的多,故D正确。
分析知,金属棒第一次下降过程磁通量的变化比第一次上升过程磁通量的变化量大,则金属棒第一次下降过程通过电阻R的电荷量比第一次上升过程的多,故D正确。

练习册系列答案
相关题目