题目内容
如图所示,两平行金属板A、B长l=8cm,两板间距离d=8cm,A板比B板电势高300V,即UAB=300V。一带正电的粒子电量q=![]() C,质量m=
C,质量m=![]() ??kg,从R点沿电场中心线垂直电场线飞入电场,初速度v0=2×106m/s,粒子飞出平行板电场后经过界面MN、PS间的无电场区域后,进入固定在中心线上的O点的点电荷Q形成的电场区域(设界面PS右边点电荷的电场分布不受界面的影响)。已知两界面MN、PS相距为L=12cm,粒子穿过界面PS最后垂直打在放置于中心线上的荧光屏EF上,O点距PS 9 cm。求(静电力常数k=9×109??N·m2/C2)
??kg,从R点沿电场中心线垂直电场线飞入电场,初速度v0=2×106m/s,粒子飞出平行板电场后经过界面MN、PS间的无电场区域后,进入固定在中心线上的O点的点电荷Q形成的电场区域(设界面PS右边点电荷的电场分布不受界面的影响)。已知两界面MN、PS相距为L=12cm,粒子穿过界面PS最后垂直打在放置于中心线上的荧光屏EF上,O点距PS 9 cm。求(静电力常数k=9×109??N·m2/C2)
求粒子从电场中飞出时的侧向位移为h
求粒子穿过界面PS时偏离中心线OR的距离为y
(3)求粒子从匀强电场中飞出时的速度v
(4)求粒子刚进入点电荷的电场时速度与其电场线的夹角??
(5)求点电荷的电量Q。
(6)若在界面PS处放一荧光屏,在两板上改加如图所示的随时间变化的电压。则由于视觉暂留和荧光物质的残光特性,则电子打在荧光屏上后会形成一个什么图形?其范围如何?

(1)3cm (2)12cm (3)![]()
(4)??=900(5)1.04×10-8C(6)在荧光屏上形成一条亮线 0.12m
解析:
(1)设粒子从电场中飞出时的侧向位移为h,
则: ![]() (1分)
(1分)
![]()
![]() 即:
即:![]() (1分)
(1分)
代入数据,解得: h=0.03m=3cm (1分)
(2)设穿过界面PS时偏离中心线OR的距离为y ,由带电粒子在离开电场后将做匀速直线运动,由相似三角形知识得:
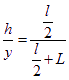 (1分)
(1分)
代入数据,解得: y=0.12m=12cm (1分)
(3)设粒子从电场中飞出时沿电场方向的速度为vy,
则:vy=at= ![]()
代入数据,解得: vy=1.5×106m/s (1分)
所以粒子从电场中飞出时沿电场方向的速度为:
![]() (1分)
(1分)
设粒子从电场中飞出时的速度方向与水平方向的夹角为θ,则:
![]()
![]() (1分)
(1分)
(4)粒子刚进入点电荷的电场时速度与其电场线的夹角??=900 (1分)
(5)设点电荷的电量Q。
因为粒子穿过界面PS最后垂直打在放置于中心线上的荧光屏上,所以该带电粒子在穿过界面PS后将绕点电荷Q作匀速圆周运动,其半径与速度方向垂直。
匀速圆周运动的半径: ![]() (1分)
(1分)
由: ![]() (2分)
(2分)
代入数据,解得: Q=1.04×10-8C (1分)
(6)因为每个电子穿过偏转电场的时间极短,所以其中任意一个电子都在偏转电场中做类平抛运动。由(2)问结果知,其侧移量与对应的电压成正比。又因为电子是连续发射,所以会在荧光屏上形成一条亮线,其长度为: y=0.12m (2分)

 阅读快车系列答案
阅读快车系列答案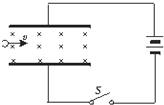 如图所示,两平行金属板水平放置,开始开关S合上使平行板电容器带电.板间存在垂直纸面向里的匀强磁场.一个不计重力的带电粒子恰能以水平向右的速度沿直线通过两板.在以下方法中,能使带电粒子仍沿水平直线通过两板的是( )
如图所示,两平行金属板水平放置,开始开关S合上使平行板电容器带电.板间存在垂直纸面向里的匀强磁场.一个不计重力的带电粒子恰能以水平向右的速度沿直线通过两板.在以下方法中,能使带电粒子仍沿水平直线通过两板的是( )| A、把两板间距离减小一半,同时把粒子速率增加一倍 | B、把两板的距离增大一倍,同时把板间的磁感应强度增大一倍 | C、把开关S断开,两板的距离增大一倍,同时把板间的磁感应强度减为一半 | D、把开关S断开,两板的距离减小一半,同时把粒子速率减小一半 |
 如图所示,两平行金属板间有一匀强电场,板长为L,板间距离为d,在 板右端L处有一竖直放置的光屏M,一带电荷量为q,质量为m的质点从两板中央射入板间,最后垂直打在M屏上,则下列结论正确的是( )
如图所示,两平行金属板间有一匀强电场,板长为L,板间距离为d,在 板右端L处有一竖直放置的光屏M,一带电荷量为q,质量为m的质点从两板中央射入板间,最后垂直打在M屏上,则下列结论正确的是( )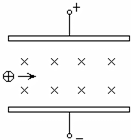 如图所示,两平行金属板中有相互垂直的匀强电场和匀强磁场,带正电的粒子(不计粒子的重力)从两板中央垂直电场、磁场入射.它在金属板间运动的轨迹为水平直线,如图中虚线所示.若使粒子飞越金属板间的过程中向上板偏移,则可以采取下列的正确措施为( )
如图所示,两平行金属板中有相互垂直的匀强电场和匀强磁场,带正电的粒子(不计粒子的重力)从两板中央垂直电场、磁场入射.它在金属板间运动的轨迹为水平直线,如图中虚线所示.若使粒子飞越金属板间的过程中向上板偏移,则可以采取下列的正确措施为( ) 如图所示,两平行金属板的间距等于极板的长度,现有重力不计的正离子束以相同的初速度v0平行于两板从两板正中间射入.第一次在两极板间加恒定电压,建立场强为E的匀强电场,则正离子束刚好从上极板边缘飞出.第二次撤去电场,在两板间建立磁感应强度为B、方向垂直于纸面的匀强磁场,正离子束刚好从下极板边缘飞出,则E和B的大小之比为( )
如图所示,两平行金属板的间距等于极板的长度,现有重力不计的正离子束以相同的初速度v0平行于两板从两板正中间射入.第一次在两极板间加恒定电压,建立场强为E的匀强电场,则正离子束刚好从上极板边缘飞出.第二次撤去电场,在两板间建立磁感应强度为B、方向垂直于纸面的匀强磁场,正离子束刚好从下极板边缘飞出,则E和B的大小之比为( ) 如图所示,两平行金属板间电场是匀强电场,场强大小为1.0×104V/m,A、B两板相距1cm,C点与A相距0.4cm,若B接地,则A、C间电势差UAC=
如图所示,两平行金属板间电场是匀强电场,场强大小为1.0×104V/m,A、B两板相距1cm,C点与A相距0.4cm,若B接地,则A、C间电势差UAC=