题目内容
 (2012?上海模拟)在动摩擦因数μ=0.2的粗糙绝缘足够长的水平滑漕中,长为2L的绝缘轻质细杆两端各连接一个质量均为m的带电小球A和B,如图为俯视图(槽两侧光滑).A球的电荷量为+2q,B球的电荷量为-3q(均可视为质点,也不考虑两者间相互作用的库仑力).现让A处于如图所示的有界匀强电场区域MPQN内,已知虚线MP恰位于细杆的中垂线,MP和NQ的距离为3L,匀强电场的场强大小为E=1.2mg/q,方向水平向右.释放带电系统,让A、B从静止开始运动(忽略小球运动中所产生的磁场造成的影响).求:
(2012?上海模拟)在动摩擦因数μ=0.2的粗糙绝缘足够长的水平滑漕中,长为2L的绝缘轻质细杆两端各连接一个质量均为m的带电小球A和B,如图为俯视图(槽两侧光滑).A球的电荷量为+2q,B球的电荷量为-3q(均可视为质点,也不考虑两者间相互作用的库仑力).现让A处于如图所示的有界匀强电场区域MPQN内,已知虚线MP恰位于细杆的中垂线,MP和NQ的距离为3L,匀强电场的场强大小为E=1.2mg/q,方向水平向右.释放带电系统,让A、B从静止开始运动(忽略小球运动中所产生的磁场造成的影响).求:(1)小球B第一次到达电场边界MP所用的时间;
(2)小球A第一次离开电场边界NQ时的速度大小
(3)带电系统运动过程中,B球电势能增加量的最大值.
分析:(1)B进入电场前的过程中,系统做匀加速运动,使用牛顿第二定律,先求出加速度,再求出运动的时间;
(2)B进入电场后前的过程中,系统做匀减速运动,使用牛顿第二定律,先求出加速度,再求出运动的时间最后求出速度.也可以使用动能定理求解;
(3)带电系统速度第一次为零,此时A已经到达右边界NQ外,B克服电场力做的功最多,B增加的电势能最多,据此列公式求出即可.
(2)B进入电场后前的过程中,系统做匀减速运动,使用牛顿第二定律,先求出加速度,再求出运动的时间最后求出速度.也可以使用动能定理求解;
(3)带电系统速度第一次为零,此时A已经到达右边界NQ外,B克服电场力做的功最多,B增加的电势能最多,据此列公式求出即可.
解答:解:
(1)带电系统开始运动后,先向右加速运动;当B进入电场区时,开始做减速运动.设B进入电场前的过程中,系统的加速度为a1,
由牛顿第二定律:2Eq-μ2mg=2ma1 即:a1=g
B刚进入电场时,由:L=
a1
可得:t1=
(2)当A刚滑到右边界时,电场力对系统做功为:W1=2Eq?2L+(-3Eq?L)=EqL
摩擦力对系统做功为:W2=-μ?2mg?2l=-0.8mgL
W总=EqL-0.8mgL=0.4mgL 故A球从右端滑出.
设B从静止到刚进入电场的速度为v1,v1=a1t1=
设B进入电场后,系统的加速度为a2,由牛顿第二定律:2Eq-3Eq-2μmg=2ma2
a2=-0.8g
系统做匀减速运动,设小球A第一次离开电场边界NQ时的速度大小为v2;
由:
-
=2a?2L,
可得:v2=
(3)当带电系统速度第一次为零,此时A已经到达右边界NQ外,B克服电场力做的功最多,B增加的电势能最多,设此时A离右边界NQ的距离为x
由动能定理:2Eq?2L-3Eq×(L+x)-μ2mg(2L+x)=0
可得:x=0.1L
所以B电势能增加的最大值△W1=3Eq×1.1L=3.3EqL=3.96mgL
答:(1)小球B第一次到达电场边界MP所用的时间
;
(2)小球A第一次离开电场边界NQ时的速度大小
;
(3)带电系统运动过程中,B球电势能增加量的最大值3.96mgL.
(1)带电系统开始运动后,先向右加速运动;当B进入电场区时,开始做减速运动.设B进入电场前的过程中,系统的加速度为a1,
由牛顿第二定律:2Eq-μ2mg=2ma1 即:a1=g
B刚进入电场时,由:L=
| 1 |
| 2 |
| t | 2 1 |
可得:t1=
|
(2)当A刚滑到右边界时,电场力对系统做功为:W1=2Eq?2L+(-3Eq?L)=EqL
摩擦力对系统做功为:W2=-μ?2mg?2l=-0.8mgL
W总=EqL-0.8mgL=0.4mgL 故A球从右端滑出.
设B从静止到刚进入电场的速度为v1,v1=a1t1=
| 2gL |
设B进入电场后,系统的加速度为a2,由牛顿第二定律:2Eq-3Eq-2μmg=2ma2
a2=-0.8g
系统做匀减速运动,设小球A第一次离开电场边界NQ时的速度大小为v2;
由:
| v | 2 2 |
| v | 2 1 |
可得:v2=
| 0.4gL |
(3)当带电系统速度第一次为零,此时A已经到达右边界NQ外,B克服电场力做的功最多,B增加的电势能最多,设此时A离右边界NQ的距离为x
由动能定理:2Eq?2L-3Eq×(L+x)-μ2mg(2L+x)=0
可得:x=0.1L
所以B电势能增加的最大值△W1=3Eq×1.1L=3.3EqL=3.96mgL
答:(1)小球B第一次到达电场边界MP所用的时间
|
(2)小球A第一次离开电场边界NQ时的速度大小
| 0.4gL |
(3)带电系统运动过程中,B球电势能增加量的最大值3.96mgL.
点评:该题情景新颖,针对同一过程的问题精致,要求我们需要对该过程减小细致的分析,才能找出正确的解题思路和方法.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
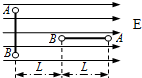 (2012?上海模拟)如图所示,绝缘杆两端固定带电小球A和B,轻杆处于水平向右的匀强电场中,不考虑两球之间的相互作用.初始时杆与电场线垂直,将杆右移的同时顺时针转过90°,发现A、B两球电势能之和不变.根据如图给出的位置关系,下列说法正确的是( )
(2012?上海模拟)如图所示,绝缘杆两端固定带电小球A和B,轻杆处于水平向右的匀强电场中,不考虑两球之间的相互作用.初始时杆与电场线垂直,将杆右移的同时顺时针转过90°,发现A、B两球电势能之和不变.根据如图给出的位置关系,下列说法正确的是( )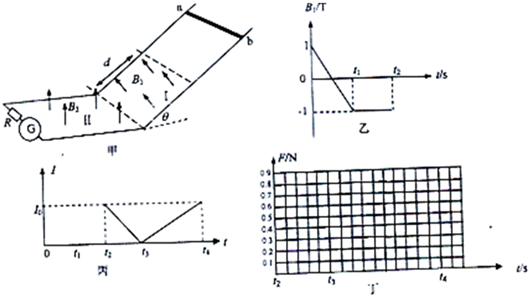
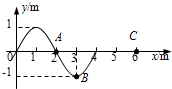 (2012?上海模拟)一列沿x正方向传播的简谐波t=0时刻的波形如图所示,t=0.2s时C点开始振动,则( )
(2012?上海模拟)一列沿x正方向传播的简谐波t=0时刻的波形如图所示,t=0.2s时C点开始振动,则( ) (2012?上海模拟)在一次国际城市运动会中,要求运动员从高为H=4m的平台上A点由静止出发,沿着动摩擦因数为μ=0.2的滑道向下运动到B点后水平滑出,最后落在水池中.滑道的水平距离L大小不变,设滑道的水平距离为L=5m,B点的高度h可由运动员自由调节,A点不动,AB长度可以调整.(取g=10m/s2) 求:
(2012?上海模拟)在一次国际城市运动会中,要求运动员从高为H=4m的平台上A点由静止出发,沿着动摩擦因数为μ=0.2的滑道向下运动到B点后水平滑出,最后落在水池中.滑道的水平距离L大小不变,设滑道的水平距离为L=5m,B点的高度h可由运动员自由调节,A点不动,AB长度可以调整.(取g=10m/s2) 求: