题目内容
 如图所示,直线MN下方无磁场,上方空间存在两个匀强磁场,其分界线是半径为R的半圆,两侧的磁场方向相反且垂直于纸面,磁感应强度大小都为B.现有一质量为m、电荷量为q的带负电微粒从P点沿半径方向向左侧射出,最终打到Q点,不计微粒的重力.求:
如图所示,直线MN下方无磁场,上方空间存在两个匀强磁场,其分界线是半径为R的半圆,两侧的磁场方向相反且垂直于纸面,磁感应强度大小都为B.现有一质量为m、电荷量为q的带负电微粒从P点沿半径方向向左侧射出,最终打到Q点,不计微粒的重力.求:(1)微粒在磁场中运动的周期;
(2)从P点到Q点,微粒的运动速度大小及运动时间;
(3)若向里磁场是有界的,分布在以O点为圆心、半径为R和2R的两半圆之间的区域,上述微粒仍从P点沿半径方向向左侧射出,且微粒仍能到达Q点,求其速度的最大值.
分析:(1)带电粒子在磁场中只受洛伦兹力,粒子在磁场中做匀速圆周运动.由牛顿第二定律和圆周运动规律求出周期.
(2)根据题意作出粒子可能的运动轨迹,由牛顿第二定律与数学知识分析答题.
(3)由几何知识分析轨迹半径的最大值,由半径公式求出速度的最大值.
(2)根据题意作出粒子可能的运动轨迹,由牛顿第二定律与数学知识分析答题.
(3)由几何知识分析轨迹半径的最大值,由半径公式求出速度的最大值.
解答:解:(1)由qvB=m
及T=
得:
微粒在磁场中运动的周期 T=
.
(2)令n表示带电粒子在磁场中运动时的圆心个数,则
由几何关系可知,微粒运动的轨道半径r应满足:r=Rtan
,(n=2,3,4,5,…),
结合(1)可知,v=
=
Rtan
,(n=2,3,4,5,…);
相应的运动轨迹所对应的圆心角φ满足:
①当n为偶数时,φ=(2π-
π)?
+
π?
=nπ;(n=2,4,6,8,…)
②当n为奇数时,φ=(2π-
π)?
+
π?
=
π;(n=3,5,7,9,…)
对应的运动时间t满足:
①当n为偶数时,t=
T=
,(n=2,4,6,8,…);
②当n为奇数时,t=
?
=
;(n=3,5,7,9,…)
(3)由几何关系可知,rn+
≤2R,(n=2,3,4,5,…);
得:当n=3时,r可取满足条件的最大值,rmax=
R,
相应的粒子速度vmax=
.
相应的运动轨迹如图所示.

答:
(1)微粒在磁场中运动的周期为
;
(2)从P点到Q点,微粒的运动速度大小为
Rtan
,(n=2,3,4,5,…);对应的运动时间;①当n为偶数时,t=
T=
,(n=2,4,6,8,…);②当n为奇数时,t=
?
=
;(n=3,5,7,9,…)
(3)速度的最大值是
.
| v2 |
| r |
| 2πr |
| v |
微粒在磁场中运动的周期 T=
| 2πm |
| qB |
(2)令n表示带电粒子在磁场中运动时的圆心个数,则
由几何关系可知,微粒运动的轨道半径r应满足:r=Rtan
| π |
| 2n |
结合(1)可知,v=
| qBr |
| m |
| qB |
| m |
| π |
| 2n |
相应的运动轨迹所对应的圆心角φ满足:
①当n为偶数时,φ=(2π-
| n-1 |
| n |
| n |
| 2 |
| n-1 |
| n |
| n |
| 2 |
②当n为奇数时,φ=(2π-
| n-1 |
| n |
| n+1 |
| 2 |
| n-1 |
| n |
| n-1 |
| 2 |
| n2+1 |
| n |
对应的运动时间t满足:
①当n为偶数时,t=
| n |
| 2 |
| nπm |
| qB |
②当n为奇数时,t=
| n2+1 |
| n |
| T |
| 2 |
| (n2+1)πm |
| nqB |
(3)由几何关系可知,rn+
| rn | ||
sin
|
得:当n=3时,r可取满足条件的最大值,rmax=
| ||
| 3 |
相应的粒子速度vmax=
| ||
| 3m |
相应的运动轨迹如图所示.

答:
(1)微粒在磁场中运动的周期为
| 2πm |
| qB |
(2)从P点到Q点,微粒的运动速度大小为
| qB |
| m |
| π |
| 2n |
| n |
| 2 |
| nπm |
| qB |
| n2+1 |
| n |
| T |
| 2 |
| (n2+1)πm |
| nqB |
(3)速度的最大值是
| ||
| 3m |
点评:此题对运动轨迹的特殊性研究到一般性探究,这是分析问题的一种方法.同时要利用圆的特性与物理规律相结合.本题是一道难题,根据题意作出粒子的运动轨迹是本题解题的难点,也是正确解题的关键.

练习册系列答案
相关题目
 如图所示,直线MN上方存在垂直纸面向里、磁感应强度大小为B的匀强磁场,现有一质量为m、带电荷量为+q的粒子在纸面内以某一速度从A点射入,其方向与MN成30°角,A点到MN的垂直距离为d,带电粒子重力不计.求:
如图所示,直线MN上方存在垂直纸面向里、磁感应强度大小为B的匀强磁场,现有一质量为m、带电荷量为+q的粒子在纸面内以某一速度从A点射入,其方向与MN成30°角,A点到MN的垂直距离为d,带电粒子重力不计.求: 如图所示,直线MN是某电场中的一条电场线(方向未画出).虚线是一带电的粒子只在电场力的作用下,由a到b的运动轨迹,轨迹为一抛物线.下列判断正确的是( )
如图所示,直线MN是某电场中的一条电场线(方向未画出).虚线是一带电的粒子只在电场力的作用下,由a到b的运动轨迹,轨迹为一抛物线.下列判断正确的是( )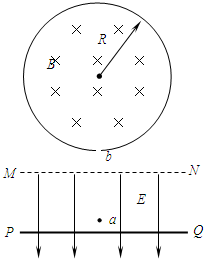 如图所示,直线MN的下方有竖直向下的匀强电场,场强大小为E=700V/m.在电场区域内有一个平行于MN的挡板PQ;MN的上方有一个半径为R=0.866m的圆形弹性围栏,在围栏区域内有图示方向的匀强磁场,磁感应强度大小为B=1.4T.围栏最低点一个小洞b,在b点正下方的电场区域内有一点a,a点到MN的距离d1=45cm,到PQ距离d2=5cm.现将一个质量为m=0.1g,带电量q=2×10-3C的带正电小球(重力不计),从a点由静止释放,在电场力作用下向下运动与挡板PQ相碰后电量减少到碰前的0.8倍,且碰撞前后瞬间小球的动能不变,不计小球运动过程中的空气阻力以及小球与围栏碰撞时的能量损失,试求:(已知1.2510=9.31,1.2511=11.628)
如图所示,直线MN的下方有竖直向下的匀强电场,场强大小为E=700V/m.在电场区域内有一个平行于MN的挡板PQ;MN的上方有一个半径为R=0.866m的圆形弹性围栏,在围栏区域内有图示方向的匀强磁场,磁感应强度大小为B=1.4T.围栏最低点一个小洞b,在b点正下方的电场区域内有一点a,a点到MN的距离d1=45cm,到PQ距离d2=5cm.现将一个质量为m=0.1g,带电量q=2×10-3C的带正电小球(重力不计),从a点由静止释放,在电场力作用下向下运动与挡板PQ相碰后电量减少到碰前的0.8倍,且碰撞前后瞬间小球的动能不变,不计小球运动过程中的空气阻力以及小球与围栏碰撞时的能量损失,试求:(已知1.2510=9.31,1.2511=11.628)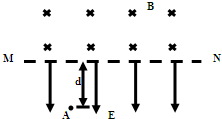 (2012?广东一模)如图所示,直线MN上方有匀强磁场,磁感应强度为B,方向垂直纸面向里;下方有方向向下的匀强电场,场强为E,一电子(电量e,质量为m)自A点由静止释放,A点到MN的距离为d.不计重力,求:
(2012?广东一模)如图所示,直线MN上方有匀强磁场,磁感应强度为B,方向垂直纸面向里;下方有方向向下的匀强电场,场强为E,一电子(电量e,质量为m)自A点由静止释放,A点到MN的距离为d.不计重力,求: