题目内容
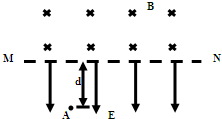 (2012?广东一模)如图所示,直线MN上方有匀强磁场,磁感应强度为B,方向垂直纸面向里;下方有方向向下的匀强电场,场强为E,一电子(电量e,质量为m)自A点由静止释放,A点到MN的距离为d.不计重力,求:
(2012?广东一模)如图所示,直线MN上方有匀强磁场,磁感应强度为B,方向垂直纸面向里;下方有方向向下的匀强电场,场强为E,一电子(电量e,质量为m)自A点由静止释放,A点到MN的距离为d.不计重力,求:(1)电子经过直线MN时速度大小;
(2)电子在磁场中运动的轨道半径;
(3)电子从A运动到第二次通过MN线时所用的时间t.
分析:(1)电子在电场中受到电场力而加速,根据牛顿第二定律和运动学公式结合求解电子经过直线MN时速度大小;
(2)电子进入磁场后,由洛伦兹力提供向心力,由牛顿第二定律求解电子在磁场中运动的轨道半径;
(3)分别求出电子在电场中匀加速运动时间和磁场中匀速圆周运动的时间.电场中,由运动学公式求解时间,磁场中根据轨迹的圆心角求解时间.
(2)电子进入磁场后,由洛伦兹力提供向心力,由牛顿第二定律求解电子在磁场中运动的轨道半径;
(3)分别求出电子在电场中匀加速运动时间和磁场中匀速圆周运动的时间.电场中,由运动学公式求解时间,磁场中根据轨迹的圆心角求解时间.
解答:解:(1)电子从A达MN界做匀加速直线运动,根据牛顿第二定律:
eE=ma 得a=
由速度-位移关系式:
-
=2as得 v=
=
(2)粒子进入磁场后做匀速圆周运动,由洛伦兹力提供向心力,根据牛顿第二定律得:
qvB=m
得到 r=
=
(3)电子从A到MN边界的过程做匀加速直线运动,历时 t1=
=
在磁场中运行半周时间:t2=
=
故电子从A运动到第二次通过MN线时所用的时间为 t=t1+t2=
+
.
答:
(1)电子经过直线MN时速度大小为
;
(2)电子在磁场中运动的轨道半径是
;
(3)电子从A运动到第二次通过MN线时所用的时间t为
+
.
eE=ma 得a=
| eE |
| m |
由速度-位移关系式:
| v | 2 t |
| v | 2 0 |
| 2ad |
|
(2)粒子进入磁场后做匀速圆周运动,由洛伦兹力提供向心力,根据牛顿第二定律得:
qvB=m
| v2 |
| r |
得到 r=
| mv |
| eB |
| 1 |
| B |
|
(3)电子从A到MN边界的过程做匀加速直线运动,历时 t1=
|
|
在磁场中运行半周时间:t2=
| T |
| 2 |
| πm |
| eB |
故电子从A运动到第二次通过MN线时所用的时间为 t=t1+t2=
|
| πm |
| eB |
答:
(1)电子经过直线MN时速度大小为
|
(2)电子在磁场中运动的轨道半径是
| 1 |
| B |
|
(3)电子从A运动到第二次通过MN线时所用的时间t为
|
| πm |
| eB |
点评:本题中电子先在电场中加速后在磁场中做匀速圆周运动,由牛顿第二定律和运动学公式结合进行研究.也可以根据动能定理求解加速获得的速度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012?广东一模)滑滑梯是小孩子很喜欢的娱乐活动.如图所示,一个小孩正在滑梯上匀速下滑,则( )
(2012?广东一模)滑滑梯是小孩子很喜欢的娱乐活动.如图所示,一个小孩正在滑梯上匀速下滑,则( ) (2012?广东一模)如图是点电荷Q周围的电场线,以下判断正确的是( )
(2012?广东一模)如图是点电荷Q周围的电场线,以下判断正确的是( ) (2012?广东一模)矩形金属线圈在匀强磁场中绕垂直于磁场的转轴匀速转动,产生的感应电动势与时间呈正弦函数关系,如图所示.此线圈与一个R=10Ω的电阻构成闭合电路,不计电路的其他电阻,下列说法正确的是( )
(2012?广东一模)矩形金属线圈在匀强磁场中绕垂直于磁场的转轴匀速转动,产生的感应电动势与时间呈正弦函数关系,如图所示.此线圈与一个R=10Ω的电阻构成闭合电路,不计电路的其他电阻,下列说法正确的是( )
 (2012?广东一模)2011年7月23日晚,雷雨交加,两列同向行驶的列车,行经浙江省温州市鹿城区黄龙街道双岙村下岙处路段高架桥面时,突然相撞--D301次动车快速追尾D3115次动车,6节车厢脱轨,3节坠落桥下(如图).在这次事故中,180余名受伤旅客成功获救,但仍有40人在这次特大铁路交通事故中遇难.事故引发公众对公共安全的高度关注.高三的小丁根据新闻进行了如下思考:火车A以对地速度v1匀速行驶,司机发现正前方同一轨道上相距s处有另一火车B沿同方向以对地速度v2(v2<v1)做匀速运动,A车司机立即以加速度a(绝对值)紧急刹车,为使两车不相撞,请求出a应满足什么条件?
(2012?广东一模)2011年7月23日晚,雷雨交加,两列同向行驶的列车,行经浙江省温州市鹿城区黄龙街道双岙村下岙处路段高架桥面时,突然相撞--D301次动车快速追尾D3115次动车,6节车厢脱轨,3节坠落桥下(如图).在这次事故中,180余名受伤旅客成功获救,但仍有40人在这次特大铁路交通事故中遇难.事故引发公众对公共安全的高度关注.高三的小丁根据新闻进行了如下思考:火车A以对地速度v1匀速行驶,司机发现正前方同一轨道上相距s处有另一火车B沿同方向以对地速度v2(v2<v1)做匀速运动,A车司机立即以加速度a(绝对值)紧急刹车,为使两车不相撞,请求出a应满足什么条件?