题目内容
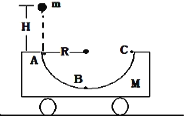
【题目】如图所示,在粗糙的水平面上放有质量为M=0.3kg的绝缘长木板,有一质量为m=0.2kg,带电量为![]() 的小滑块(可视为质点)正沿木板的上表面向左运动,木板左端有一个固定的、半径R=0.1m的四分之一光滑圆形绝缘轨道AB与之相接,轨道的最低点B点与木板的上表面相切,整个空间加有一个方向竖直向上、场强大小为
的小滑块(可视为质点)正沿木板的上表面向左运动,木板左端有一个固定的、半径R=0.1m的四分之一光滑圆形绝缘轨道AB与之相接,轨道的最低点B点与木板的上表面相切,整个空间加有一个方向竖直向上、场强大小为![]() 的匀强电场。已知滑块与木板间的动摩擦因数为
的匀强电场。已知滑块与木板间的动摩擦因数为![]() ,木板与水平面间的动摩擦因数
,木板与水平面间的动摩擦因数![]() ,滑块在木板上向左运动至离B点x=0.3m处时速度大小为
,滑块在木板上向左运动至离B点x=0.3m处时速度大小为![]() ,
,![]() ,求
,求
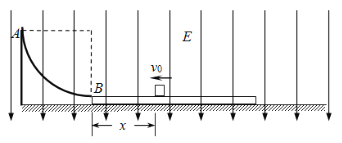
(1)滑块通过木板滑上固定的光滑圆形轨道AB,沿轨道AB上升的最大高度H
(2)滑块沿轨道AB返回刚运动至B点时对轨道的压力
(3)若木板长度为0.6m,试求滑块再次返回滑上木板,而在木板上运动的过程中,系统因摩擦而产生的热量
【答案】(1)![]() (2)NB.=42牛,方向竖直向下(3)0.627J
(2)NB.=42牛,方向竖直向下(3)0.627J
【解析】
试题(1)(4分)对于滑块上升到最高点过程,据动能定理得:]![]()
解得:![]() m
m
(2)(6分)对于滑块从开始运动到返回至B点处过程,
据动能定理得:![]()
在B点由牛顿第二定律:![]() 解得:vb=3m/s NB=22N
解得:vb=3m/s NB=22N
由牛顿第三定律:滑块对轨道的压力的大小为NB.=42牛,方向竖直向下
(3)(9分)滑块再次滑上木板后,由于f1=μ1(mg+qE)=1N, f2=μ2(qE+mg+Mg)=0.7N
则μ1(mg+qE)>μ2(qE+mg+Mg) 所以木板将由静止开始做匀加速运动,滑块做匀减速运动。
又木块加速度大小:a1=![]() =1m/s2 滑块的加速度大小:a2=
=1m/s2 滑块的加速度大小:a2=![]() =5m/s2
=5m/s2
设两者经过时间t0速度相等,则 vB-a2t0=a1t0,解得,t0=0.5s
则在两者相对滑动的过程中,木板的位移为s1=![]() =0.125m
=0.125m
滑块的位移为s2=![]() =0.875m 由于△s=s1-s2=0.75m>木板的长度L=0.6m
=0.875m 由于△s=s1-s2=0.75m>木板的长度L=0.6m
故滑块在二者速度相等之前就要离开木板
设滑块经过时间t离开木板,则:
![]() —
—![]() =L
=L
![]() s 木板位移
s 木板位移![]() m
m
故系统因摩擦而产生的热量Q= f1L+ f2 ![]() =0.627J
=0.627J

 阅读快车系列答案
阅读快车系列答案