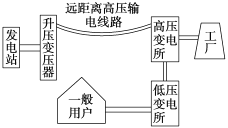
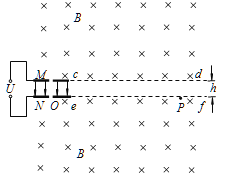题目内容
【题目】如图所示，质量为1.0g的带电小球，用长为L的绝缘细线悬挂在平行板电容器之间，两板电压为40V，板间距10cm，小球在A点处于平衡状态．悬线和竖直方向夹角为α=370(sin370=0.6，cos370=0.8，g取10 m/s2)．则：
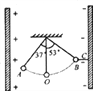
(1)请判断小球的电性并求出电量；
(2)若通过另一绝缘细线BC把该小球缓慢拉到另一侧的B点（B点未触及右极板)，平衡时悬线与竖直方向夹角为β=530，细线BC呈水平，则此时细线BC中的拉力为多大?
(3)在(2)中，若把BC细线剪断，小球摆回到最低点O时，悬线对小球的拉力有多大?
【答案】（1）
（2）
（3）0.03N
【解析】试题分析：根据小球受力平衡求出小球所受的电场力，进而判断小球的电性计算小球的带电量；在B点对小球进行受力分析即可求得水平线BC的拉力；先根据动能定理求出小球到达O时的速度，再根据向心力公式求解悬线拉力。
电容器板间场强为： 
，小球所受的电场力向
左，场强向右，故小球带负电；对小球在A点的受力进行分析，小球受重力、细线的拉力和电场力，如左图所示：
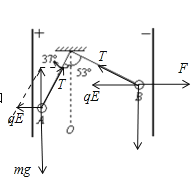
根据共点力平衡条件，有
代入数据解得： 
（2）在B点，设水平拉力为T，绳的拉力为F，受力分析，如图所示：
根据共点力平衡条件，有: 
联立解得：
（3）从B点到小球摆到最低点O的过程中运用动能定理得：
根据牛顿第二定律，得： 
解得： 
练习册系列答案
相关题目
