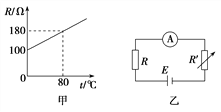
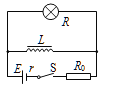
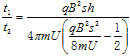题目内容
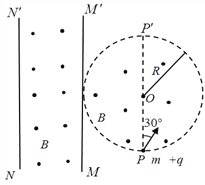
【题目】某种粒子加速器的设计方案如图19所示,M、N为两块垂直于纸面旋转放置的圆形正对平行金属板,两金属板中心均有小孔(孔的直径大小可忽略不计),板间距离为h。两板间接一直流电源,每当粒子进入M板的小孔时,控制两板的电势差为U,粒子得到加速,当粒子离开N板时,两板的电势差立刻变为零。两金属板外部存在着上、下两个范围足够大且有理想平面边界的匀强磁场,上方磁场的下边界cd与金属板M在同一水平面上,下方磁场的上边界ef与金属板N在同一水平面上,两磁场平行边界间的距离也为h,磁场方向垂直纸面向里,磁感应强度为B。在两平行金属板右侧形成与金属板间距离一样为h的无电场、无磁场的狭缝区域。一质量为m、电荷量为q的带正电粒子从M板小孔处无初速度释放,粒子在MN板间被加速,粒子离开N板后进入下方磁场中运动。若空气阻力、粒子所受的重力以及粒子在运动过程中产生的电磁辐射均可忽略不计,不考虑相对论效应、两金属板间电场的边缘效应以及电场变化对于外部磁场和粒子运动的影响。
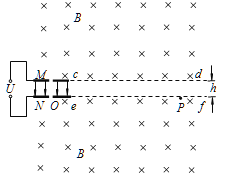
(1)为使带电粒子经过电场加速后不打到金属板上,请说明圆形金属板的半径R应满足什么条件;
(2)在ef边界上的P点放置一个目标靶,P点到N板小孔O的距离为s时,粒子恰好可以击中目标靶。对于击中目标靶的粒子,求:
①其进入电场的次数n;
②其在电场中运动的总时间与在磁场中运动的总时间之比。
【答案】(1)R<![]() ;(2)①
;(2)①![]() ;②
;②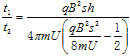 。
。
【解析】(1)设粒子第一次经过电场加速后的速度为v1,
对于这个加速过程,根据动能定理有:![]() ,解得
,解得![]() ;
;
粒子进入磁场中做匀速圆周运动,设其运动的轨道半径为r1,
根据洛伦兹力和牛顿第二定律有:![]() ,
,
得![]()
为使粒子不打到金属板上,应使金属板的半径R<2r1,即R<![]()
(2)①设到达ef边界上P点的粒子运动速度为vn,根据几何关系可知,其在磁场中运动的最后一周的轨道半径rn=s/2,
根据洛伦兹力公式和牛顿第二定律有 ![]() ,
,
解得![]()
设粒子在电场中被加速n次,对于这个加速过程根据动能定理有![]()
解得:![]() 。
。
②设粒子在电场中运动的加速度为a,根据牛顿第二定律有:![]() ,
,
解得![]()
因在磁场中运动洛伦兹力不改变粒子运动速度的大小,故粒子在电场中的间断加速运动可等效成一个连续的匀加速直线运动
设总的加速时间为t1,根据vn=at1
可得![]()
粒子在磁场中做匀速圆周运动,运动周期 ![]() 保持不变
保持不变
对于击中目标靶的粒子,其在磁场中运动的总时间
t2=![]() 所以
所以