题目内容
1.“嫦娥三号”探测卫星被月球引力场俘获后,在月球表面轨道运行,要估算月球的密度,唯一要测量的物理量是( )| A. | 月球的半径 | B. | “嫦娥三号”的轨道半径 | ||
| C. | 月球的公转周期 | D. | “嫦娥三号”的公转周期 |
分析 对飞船受力分析,万有引力提供向心力,根据牛顿第二定律列式,求解出密度表达式分析即可.
解答 解:飞船靠近月球,在靠近月球表面做匀速圆周运动,轨道半径等于月球半径,设为r,根据牛顿第二定律,有:
G$\frac{Mm}{{r}^{2}}$=m($\frac{2π}{T}$)2
其中:
M=ρV=ρ•$\frac{4}{3}$πr3
联立解得:
ρ=$\frac{3π}{G{T}^{2}}$,G为常数,故需要测量卫星的公转周期T;
故选:C
点评 对于星球表面的卫星,靠万有引力提供向心力,有ρT2=$\frac{3π}{G}$(常数)的结论,可以记住,不难.

练习册系列答案
相关题目
20.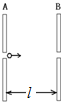 如图所示,A、B是一对中间开有小孔的平行金属板,两小孔的连线与金属板相垂直,两极板的间距为l.两极板间加上低频交流电压,A板电势为零,B板电势φ=φ0sinωt(其中φ0>0).现有一电子在某时刻穿过A板上的小孔进入电场,设初速度和重力的影响均可忽略不计.下列说法正确的是( )
如图所示,A、B是一对中间开有小孔的平行金属板,两小孔的连线与金属板相垂直,两极板的间距为l.两极板间加上低频交流电压,A板电势为零,B板电势φ=φ0sinωt(其中φ0>0).现有一电子在某时刻穿过A板上的小孔进入电场,设初速度和重力的影响均可忽略不计.下列说法正确的是( )
 如图所示,A、B是一对中间开有小孔的平行金属板,两小孔的连线与金属板相垂直,两极板的间距为l.两极板间加上低频交流电压,A板电势为零,B板电势φ=φ0sinωt(其中φ0>0).现有一电子在某时刻穿过A板上的小孔进入电场,设初速度和重力的影响均可忽略不计.下列说法正确的是( )
如图所示,A、B是一对中间开有小孔的平行金属板,两小孔的连线与金属板相垂直,两极板的间距为l.两极板间加上低频交流电压,A板电势为零,B板电势φ=φ0sinωt(其中φ0>0).现有一电子在某时刻穿过A板上的小孔进入电场,设初速度和重力的影响均可忽略不计.下列说法正确的是( )| A. | 若电子在t=0时刻穿过A板上的小孔进入电场,则电子在两极板间可能以AB间的某一点为中心来回振动 | |
| B. | 若电子在t=$\frac{π}{2ω}$时刻穿过A板上的小孔进入电场,则电子在两极板间可能以AB间的某一点为中心来回振动 | |
| C. | 若电子在t=0时刻穿过A板上的小孔进入电场,则不论ω,l为何值,电子在两极板间都一定是一直向B板运动,最后穿出B板 | |
| D. | 若电子在t=$\frac{π}{2ω}$时刻穿过A板上的小孔进入电场,电子可能一直向B板运动,最后穿出B板 |
9.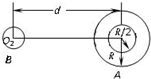 如图所示,铅球A的半径为R,质量为M,另一质量为m的铅球B,两球球心的距离为d,设两铅球之间的万有引力为F.若在铅球A的内部挖去一个半径为$\frac{R}{2}$的球形空腔,空腔的球心在A的球心处,则挖去之后两物体间的万有引力为( )
如图所示,铅球A的半径为R,质量为M,另一质量为m的铅球B,两球球心的距离为d,设两铅球之间的万有引力为F.若在铅球A的内部挖去一个半径为$\frac{R}{2}$的球形空腔,空腔的球心在A的球心处,则挖去之后两物体间的万有引力为( )
 如图所示,铅球A的半径为R,质量为M,另一质量为m的铅球B,两球球心的距离为d,设两铅球之间的万有引力为F.若在铅球A的内部挖去一个半径为$\frac{R}{2}$的球形空腔,空腔的球心在A的球心处,则挖去之后两物体间的万有引力为( )
如图所示,铅球A的半径为R,质量为M,另一质量为m的铅球B,两球球心的距离为d,设两铅球之间的万有引力为F.若在铅球A的内部挖去一个半径为$\frac{R}{2}$的球形空腔,空腔的球心在A的球心处,则挖去之后两物体间的万有引力为( )| A. | $\frac{1}{2}F$ | B. | $\frac{3}{4}F$ | C. | $\frac{7}{8}F$ | D. | $\frac{15}{16}F$ |
6.若汽车受到的摩擦阻力大小不变,则以下关于汽车运动的分析中正确的是( )
| A. | 若汽车做匀速直线运动,则其发动机的功率将保持不变 | |
| B. | 若汽车做匀加速直线运动,则其发动机的功率将逐渐增大 | |
| C. | 若汽车做匀速直线运动,则其发动机的功率将逐渐增大 | |
| D. | 汽车上坡时一定要增大发动机的功率 |
11.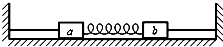 如图所示,将两相同的木块a、b置于粗糙的水平地面上,中间用一轻弹簧连接,两侧用细绳固定于墙壁.开始时a、b均静止,弹簧处于伸长状态,两细绳均有拉力,a所受摩擦力Ffa≠0,b所受摩擦力Ffb=0,现将右侧细绳剪断,则剪断瞬间( )
如图所示,将两相同的木块a、b置于粗糙的水平地面上,中间用一轻弹簧连接,两侧用细绳固定于墙壁.开始时a、b均静止,弹簧处于伸长状态,两细绳均有拉力,a所受摩擦力Ffa≠0,b所受摩擦力Ffb=0,现将右侧细绳剪断,则剪断瞬间( )
 如图所示,将两相同的木块a、b置于粗糙的水平地面上,中间用一轻弹簧连接,两侧用细绳固定于墙壁.开始时a、b均静止,弹簧处于伸长状态,两细绳均有拉力,a所受摩擦力Ffa≠0,b所受摩擦力Ffb=0,现将右侧细绳剪断,则剪断瞬间( )
如图所示,将两相同的木块a、b置于粗糙的水平地面上,中间用一轻弹簧连接,两侧用细绳固定于墙壁.开始时a、b均静止,弹簧处于伸长状态,两细绳均有拉力,a所受摩擦力Ffa≠0,b所受摩擦力Ffb=0,现将右侧细绳剪断,则剪断瞬间( )| A. | Ffa大小不变 | B. | Ffa方向改变 | C. | Ffb方向向右 | D. | Ffb仍然为零 |
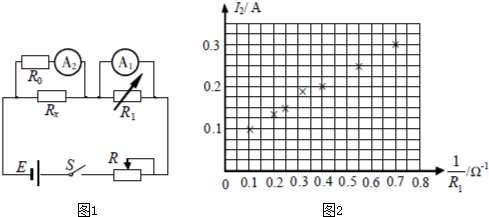

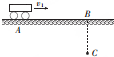 如图所示,公路上一辆汽车(可看成质点)以v1=12m/s的速度匀速行驶,汽车行至A点时,某人为搭车,从距公路30m远的C处开始以v2=3m/s的速度正对公路匀速跑去,司机见状途中刹车,汽车做匀减速直线运动,结果车停在B点时,人同时到达B点.已知A、B间的距离x=100m.试求:
如图所示,公路上一辆汽车(可看成质点)以v1=12m/s的速度匀速行驶,汽车行至A点时,某人为搭车,从距公路30m远的C处开始以v2=3m/s的速度正对公路匀速跑去,司机见状途中刹车,汽车做匀减速直线运动,结果车停在B点时,人同时到达B点.已知A、B间的距离x=100m.试求: