题目内容
【题目】如图所示，光滑半球的半径为R，球心为O，固定在水平面上，其上方有一个光滑曲面轨道AB，高度为R/2．轨道底端水平并与半球顶端相切．质量为m的小球由A点静止滑下．小球在水平面上的落点为C（重力加速度为g），则（ ）
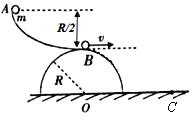
A．将沿半球表面做一段圆周运动后抛至C点
B．小球将从B点开始做平抛运动到达C点
C．OC之间的距离为
R
D．小球从A运动到C的时间等于（1+）
【答案】BC
【解析】
试题分析：从A到B的过程中，根据机械能守恒可，mg
R=mV2，解得
，在B点，当重力恰好作为向心力时，由
，解得
，所以当小球到达B点时，重力恰好作为向心力，所以小球将从B点开始做平抛运动到达C，所以A错误，B正确．根据平抛运动的规律，水平方向上：x=VBt
竖直方向上：R=gt2 ；解得x=
R，
； 所以C正确；由A到C过程时物体先做变速曲线运动，再做平抛运动，平抛运动的时间； 根据给出的答案可知，求出的曲线运动时间
，很明显是利用了
除以
，而实际情况是物体沿圆弧运动，经过的路程不是，同时平均速度也不是，所以求出的结果一定是错误的，故D错误．故选BC．
练习册系列答案
相关题目
