题目内容
【题目】如图所示,传送带长L=9m,与水平方向的夹角θ=37°,以v0=5m/s的恒定速度向上运动.一个质量为m=2kg的物块(可视为质点),沿平行于传送带方向以v1=10m/s的速度滑上传送带,已知物块与传送带之间的动摩擦因数=0.5,sin 37°=0.6,cos 37°=0.8,g=10m/s2 . 求: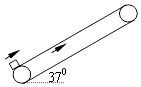
(1)物块刚滑上传送带时的加速度a
(2)物块到达传送带顶端时的速度v.
【答案】
(1)解:物块刚滑上传送带时,物块的加速度大小为a1,由牛顿第二定律有:
mgsin37°+μmgcos37°=ma1
代入数据解得: ![]() ;
;
答:物块刚滑上传送带时的加速度a为10m/s2,方向沿斜面向下
(2)解:设物块速度减为5m/s所用时间为t1,则v0﹣v=a1t1
解得:t1=0.5s
通过的位移: ![]() m<9 m
m<9 m
因μ<tanθ,此后物块继续减速上滑的加速度大小为a2则:mgsin37°﹣μmgcos37°=ma2
代入数据解得: ![]()
设物块到达最高点的速度为v1,则:v2﹣v12=2a2x2
x2=l﹣x1=5.25m
解得:v1=2m/s,方向沿斜面向上
答:物块到达传送带顶端时的速度v为2m/s,方向沿斜面向上.
【解析】(1)物块刚滑上传送带时对物体进行受力分析,注意摩擦力是与相对运动的方向相反。
(2)所有传送带类问题一定要注意物体与传送带共速,此时物体与传送带之间摩擦力消失。
【考点精析】认真审题,首先需要了解滑动摩擦力(滑动摩擦力:利用公式f=μF N 进行计算,其中FN 是物体的正压力,不一定等于物体的重力,甚至可能和重力无关.或者根据物体的运动状态,利用平衡条件或牛顿定律来求解).

练习册系列答案
相关题目