题目内容
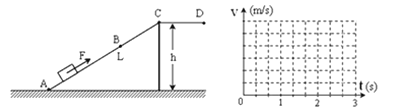
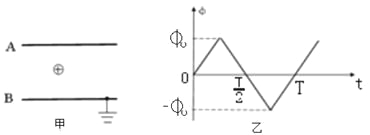
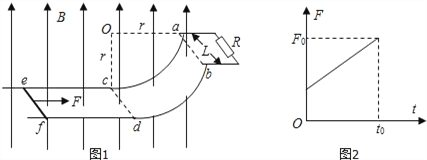
【题目】如图1所示，两根水平的金属光滑平行导轨，其末端连接等高光滑的
圆弧，其轨道半径r=0.5m，圆弧段在图中的cd和ab之间，导轨的间距为L=0.5m，轨道的电阻不计，在轨道的顶端接有阻值为R=2.0Ω的电阻，整个装置处在竖直向上的匀强磁场中，磁感应强度B=2.0T．现有一根长度稍大于L、电阻不计，质量m=1.0kg的金属棒，从轨道的水平位置ef开始在拉力F作用下，从静止匀加速运动到cd的时间t0=2.0s，在cd时的拉力为F0=3.0N．已知金属棒在ef和cd之间运动时的拉力随时间变化的图象如图2所示，重力加速度g=10m/s2，求：
(1)求匀加速直线运动的加速度；
(2)金属棒做匀加速运动时通过金属棒的电荷量q；
(3)匀加到cd后，调节拉力使金属棒接着沿圆弧做匀速圆周运动至ab处，金属棒从cd沿圆弧做匀速圆周运动至ab的过程中，拉力做的功W．
【答案】（1）1．5m/s2（2）1．5C（3）5．59J
【解析】试题分析：（1）设金属棒匀加速运动的加速度为a，则运动到cd的速度：v=2a
当金属棒在cd时为研究对象，产生的感应电动势：E=BLv
产生的电流：
金属棒所受的安培力：F=BIL
据牛顿第二定律得：F0﹣F=ma
联立以上带入数据解得：a=1．5m/s2①
（2）据以上可知，金属棒匀加速运动的位移：s=
at2②
据法拉第电磁感应定律得：
③
通过金属棒的平均电流：
④
通过金属棒的电量：q=I1△t ⑤
联立①②③④⑤带入数据解得：q=1．5C
（3）金属棒在圆弧轨道的速率：v=at=3m/s ⑥
运动的时间为：
⑦
产生的电动势最大值：Em=BLv ⑧
由于圆弧段导体棒做的是匀速圆周运动，所以导体棒中产生正弦式电流，所以产生的热量：
⑨
据能量守恒可知：W=Q+mgh （10）
联立以上解得：W=5．59J
