��Ŀ����
С��վ��ˮƽ�����ϣ����ղ����쳤������һ�ˣ�������һ��ϵ������Ϊm��С��˦������ʹ������ֱƽ������Բ���˶�������ij���˶�����͵�ʱ����ǡ�öϵ��������ˮƽ����d����أ���ͼ��ʾ����֪�������������߶�Ϊd��������֮�������Ϊ d���������ٶ�Ϊg�������ֵ��˶��뾶�Ϳ������������ܳ��ܵ��������Ϊ��ֵ��
d���������ٶ�Ϊg�������ֵ��˶��뾶�Ϳ������������ܳ��ܵ��������Ϊ��ֵ��

��1�������Ͽ�ʱС����ٶȣ�
��2�������ܳ��ܵ�����������
��3�����ֵ�λ��ʼ�ղ��䣬�ı�����ʹ��������������Ϊ ��Ҫʹ���������˶�����͵�ʱǡ�öϵ�����С����е�ˮƽ���룮
��Ҫʹ���������˶�����͵�ʱǡ�öϵ�����С����е�ˮƽ���룮
 d���������ٶ�Ϊg�������ֵ��˶��뾶�Ϳ������������ܳ��ܵ��������Ϊ��ֵ��
d���������ٶ�Ϊg�������ֵ��˶��뾶�Ϳ������������ܳ��ܵ��������Ϊ��ֵ��
��1�������Ͽ�ʱС����ٶȣ�
��2�������ܳ��ܵ�����������
��3�����ֵ�λ��ʼ�ղ��䣬�ı�����ʹ��������������Ϊ
 ��Ҫʹ���������˶�����͵�ʱǡ�öϵ�����С����е�ˮƽ���룮
��Ҫʹ���������˶�����͵�ʱǡ�öϵ�����С����е�ˮƽ���룮��1�����Ͽ�ʱС����ٶ�Ϊ ��
��
��2�����ܳ��ܵ��������Ϊ mg��
mg��
��3��С����е�ˮƽ����Ϊ ��
��
 ��
����2�����ܳ��ܵ��������Ϊ
 mg��
mg����3��С����е�ˮƽ����Ϊ
 ��
�������������1�����Ϻ�С����ƽ���˶�������ƽ���˶��ĸ߶����ʱ�䣬����ˮƽλ�ƺ�ʱ���������ʱ����ٶȴ�С��
��2����������͵㣬�����ṩ������������ţ�ٵڶ�����������������
��3���ȸ���ţ�ٵڶ����������͵��ٶȣ�Ȼ�����ƽ���˶��ķ�λ�ƹ�ʽ��ʽ�����̣�
��1�������Ϻ�����ƽ���˶���ʱ��Ϊt1��
��ֱ�����ϣ�
 d=
d= gt12��ˮƽ�����ϣ�d=v1t1
gt12��ˮƽ�����ϣ�d=v1t1���v1=
 ��
����2�������ܳ��ܵ��������ΪFm��
����Բ���˶��İ뾶ΪR=
 d
dFm��mg="m"

���Fm=
 mg
mg��3����ԭ�ܵ���͵㣬�У�Fm��mg=m

ƽ���˶����У�
d��
 =
=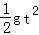
s=vt
������ã�s=

�����������ۺ���ƽ���˶���Բ���˶������˶����ؼ�֪��ƽ���˶�����ֱ�����ˮƽ�����ϵ��˶����ɣ��Լ�Բ���˶�����������Դ��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ

 �İ��ˣ�����ʱС��ij���Ϊ
�İ��ˣ�����ʱС��ij���Ϊ ʱ��������ǡ��ѹ����������˵������ȷ���ǣ�
ʱ��������ǡ��ѹ����������˵������ȷ���ǣ�


 ��
��


 ��(���ʰ뾶������,��������һ�㸽����֮�غϵ�Բ�������뾶)��ô����˵����ȷ���ǣ� ��
��(���ʰ뾶������,��������һ�㸽����֮�غϵ�Բ�������뾶)��ô����˵����ȷ���ǣ� ��





