题目内容
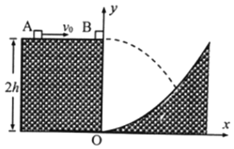
【题目】如图所示，光滑水平台面左端有一小物块A，右端有一小物块B，右侧面与一曲面相连。以台面右侧底端的O点为原点建立坐标系Oxy．已知，台面的高度为2h，曲面的方程为y=
x2，物块A的质量是物块B质量的n倍，A物块以速度v0向右运动与物块B发生弹性正碰，碰撞后物块B沿水平方向飞出，忽略空气阻力，重力加速度为g。
（1）求碰撞后瞬间物块B的速度大小；
（2）n值不同，物块B落到曲面时的动能也不同。求n取多大时，物块B落到曲面时动能最小。
【答案】（1）
v0（2）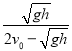
【解析】
(1)设B的质量为m，则A的质量为nm。对于碰撞过程，取向右为正方向，根据动量守恒定律得：nmv0=nmv1+mv2
根据机械能守恒定律得：
nmv02=nmv12+mv22
解得碰撞后瞬间物块B的速度大小：
v2=
v0
(2)设物块B落到曲面时下落的高度为H，水平位移为x，则H=
，x=v2t，
则落到C点时，对应的坐标为y=2h-H，x=v2t，
根据曲面的方程y=
x2，
解得：
2h-H=（v2t）2
B平抛过程，根据动能定理得：mgH=
-mv22
联立得物块B落到曲面时动能：
=
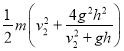
上式可以整理为：
=
可知当
即：
时物块B的动能最小。
联立可得：
n=
练习册系列答案
名校课堂系列答案
相关题目
