��Ŀ����
����Ŀ����ͼ��ʾ�����ΪL���費�Ƶ��㹻��˫б����ƽ�е��죬��⻬���ҵ���ֲڣ����ҵ���ֱ���ˮƽ��ɦ����½ǣ��ֱ��д�ֱ�ڵ���б�����ϵĴŸ�Ӧǿ��ΪB1 �� B2�����ٴų��������Ĵų�����Ӱ�죬������Ϊm�������Ϊr�ĵ����ab��cd����ƽ�е��촹ֱ�����ҽӴ����ã�ab���ɾ�ֹ�ͷţ�cd��ʼ�վ�ֹ��������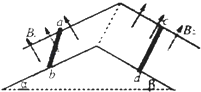
��1��ab���ٶȴ�СΪvʱͨ��cd�ĵ�����С��cd���ܵ���Ħ������С��
��2��ab�������˶�ʱ�ٶȴ�С����ʱcd�����ĵĵ繦�ʣ�
���𰸡�
��1���⣺�������ab���ٶ�Ϊvʱ�����и�Ÿ��߲����ĸ�Ӧ�綯�ƴ�СΪ��
E=B1Lv����
�����ab��cd��������ȫ��·ŷķ�����У�
I= ![]() ����
����
�����٢�ʽ������������cd�ĵ�����СΪ��
I= ![]() ����
����
�����cd���ܰ�����Ϊ��F2=B2IL����
��mgsin�£�F2����Ħ������СΪ��
f1=mgsin�©�F2=mgsin�©� ![]() ����
����
��mgsin�¡�F2����Ħ������СΪ��
f2=F2��mgsin��= ![]() ��mgsin�¡���
��mgsin�¡���
�� ab���ٶȴ�СΪvʱͨ��cd�ĵ�����СΪ ![]() ��cd���ܵ���Ħ������СΪmgsin�©�
��cd���ܵ���Ħ������СΪmgsin�©� ![]() ��
�� ![]() ��mgsin�£���2��ab�������˶�ʱ�ٶȴ�С����ʱcd�����ĵĵ繦�ʣ�
��mgsin�£���2��ab�������˶�ʱ�ٶȴ�С����ʱcd�����ĵĵ繦�ʣ�
��2���赼���ab�����˶�ʱ�ٶ�Ϊv0����ʱ�����ab�����ĸ�Ӧ�綯��Ϊ��
E0=B1Lv0����
���������ab�ĵ�����СΪ��
I0= ![]() ����
����
�����ab���ܰ�����Ϊ��F1=B1I0L����
�����ab�����˶������㣺mgsin����F1=0����
�����ߢ���ʽ��ã�v0= ![]()
��ʱcd�����ĵĵ繦��Ϊ��P= ![]() r=
r= ![]()
�� ab�������˶�ʱ�ٶȴ�СΪ ![]() ����ʱcd�����ĵĵ繦��Ϊ
����ʱcd�����ĵĵ繦��Ϊ ![]() ��
��
����������1���ȸ������ֶ����������Ӧ�綯�ƵĴ�С���ٽ�ϱպϵ�·ŷķ�����Լ���������ʽ������⡣
��2�������������ֱ���˶�ʱ������ƽ�ⷽ�̼���������ʽ ������⼴�ɡ�