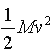��Ŀ����
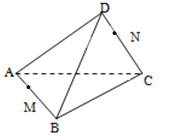
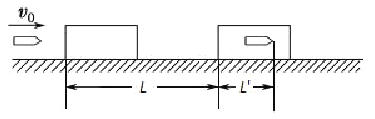
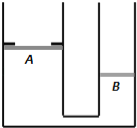
����Ŀ����ͼ��ʾ����A����v0��4m/s��ˮƽ�ٶ��׳�һ����m��1kg��С��飨����Ϊ�ʵ㣩��������˶���B��ʱ��ǡ�������߷������⻬Բ�����BC����Բ�����������C��ȸߡ���ֹ�ڴֲ�ˮƽ��ij�ľ���ϣ��뻡���C������ˮƽ����֪��ľ�������M��4kg��A��B�����C��ĸ߶ȷֱ�ΪH��0��6m��h��0��15m��R��0��75m������볤ľ��֮��Ķ�Ħ������![]() ��0��5����ľ��������Ķ�Ħ������
��0��5����ľ��������Ķ�Ħ������![]() ��0��2��gȡ10m/s2����
��0��2��gȡ10m/s2����
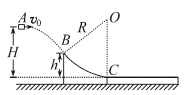
��1��С����˶���B��ʱ���ٶȴ�С�ͷ���
��2��С��黬����C��ʱ�ܵ�Բ�����������֧������С��
��3����ľ������Ϊ������ܱ�֤С��鲻������ľ�塣
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]()
�������������������1�������A��B��ƽ���˶�,y����![]()
����B��ʱ��![]()
��![]() ������ˮƽ��ļн�Ϊ
������ˮƽ��ļн�Ϊ![]() ,��
,��![]()
![]()
��2����A��C��,�ɶ��ܶ����ã�![]()
��С�����C���ܵ���֧����Ϊ![]() ,��ţ�ٵڶ����ɵã�
,��ţ�ٵڶ����ɵã�![]()
������ã�![]() ��
��
��3��С���Գ�ľ���Ħ����Ϊ![]() ,��ľ������������Ħ�������Ƶ��ڻ���Ħ����
,��ľ������������Ħ�������Ƶ��ڻ���Ħ����![]() ,��
,��![]() ,����С����ڳ�ľ���ϻ���ʱ,��ľ�徲ֹ������С����ڳ�ľ�������ȼ����˶�,����ľ���Ҷ�ʱ�ٶȸպ�Ϊ0,��ľ�峤������Ϊ��
,����С����ڳ�ľ���ϻ���ʱ,��ľ�徲ֹ������С����ڳ�ľ�������ȼ����˶�,����ľ���Ҷ�ʱ�ٶȸպ�Ϊ0,��ľ�峤������Ϊ��![]() ��
��

��ϰ��ϵ�д�
�����Ŀ