题目内容
如图所示,带电平行金属板PQ和MN之间的距离为d,两金属板之间有垂直纸面向里的匀强磁场,磁感应强度大小为B,如图建立坐标系,x轴平行于金属板,与金属板中心线重合,y轴垂直于金属板。区域I的左边界在y轴,右边界与区域II的左边界重合,且与y轴平行;区域II的左、右边界平行。在区域I和区域II内分别存在匀强磁场,磁感应强度大小均为B,区域I内的磁场垂直于Oxy平面向外,区域II内的磁场垂直于Oxy平面向里。一电子沿着x轴正向以速度v0射入平行板之间,在平行板间恰好沿着x轴正向做直线运动,并先后通过区域I和Ⅱ。已知电子电量为e,质量为m,区域I和区域II沿x轴方向宽度均为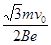 ,不计电子所受重力。
,不计电子所受重力。
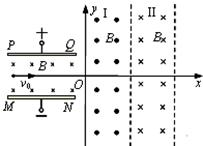
(1)求两金属板之间电势差U
(2)求电子从区域II右边界射出时,射出点的纵坐标y
【答案】
(1)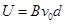 (2)
(2) 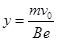
【解析】
试题分析:(1)由于粒子进入平行板电容器正好做直线运动,证明洛伦兹力等于电场力即
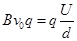 ,即
,即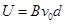
(2)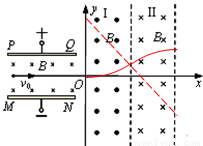 电子的运动轨迹如图,根据洛伦兹力提供向心力则有
电子的运动轨迹如图,根据洛伦兹力提供向心力则有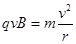 ,即
,即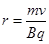 ,设在I磁场区域上升高度为h,设磁场宽度为D根据几何知识
,设在I磁场区域上升高度为h,设磁场宽度为D根据几何知识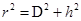 ,
,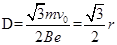 ,则求得
,则求得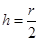 由对称性可知,在II磁场中升高高度也为
由对称性可知,在II磁场中升高高度也为 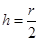 ,所以射出时纵坐标为
,所以射出时纵坐标为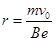
考点:洛伦兹力提供向心力、数理结合
点评:此类题型考察了速度选择器并结合带电粒子在磁场中的运动,结合勾股定理从而确定粒子的轨迹

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 )如图13所示,两块平行金属板A、B水平放置,板间距离为d,两金属板分别与电源的正、负极相连接。在距离B板d/2处的O点有一个质量为m的带电液滴恰好保持静止状态,液滴所带电荷为q。
)如图13所示,两块平行金属板A、B水平放置,板间距离为d,两金属板分别与电源的正、负极相连接。在距离B板d/2处的O点有一个质量为m的带电液滴恰好保持静止状态,液滴所带电荷为q。 cm。
cm。
 v0大小;
v0大小; cm。
cm。
