题目内容
）如图13所示，两块平行金属板A、B水平放置，板间距离为d，两金属板分别与电源的正、负极相连接。在距离B板d/2处的O点有一个质量为m的带电液滴恰好保持静止状态，液滴所带电荷为q。
（1）求电源的电动势。
（2）若保持两金属板与电源的连接，将A极板向上移动使两极板间的距离增
大到2d，液滴将会向哪个极板运动？A板上移后，液滴从O点由静止开始释
放，经过多长时间能到达极板上？
（3）若将两板竖直放置，保持电源电动势及两板间的距离d不变，将该液滴仍
从两金属板间的中点位置由静止释放，设金属板足够长。求该液滴运动到达金
属板上的速度大小。
（1）
（2）t =
（3）v =
解析:
（1）液滴处于静止状态，受力平衡，设电源电动势为E，则：
= mg， （2分）
解得：E =
。 （2分）
（2）将A极板向上移动使两极板间的距离增大到2d，电场强度变小，电场强度变小，电场力减小，液滴向B板运动。 （2分）
设液滴的加速度为a，根据牛顿第二定律
mg –
， （2分）
设液滴运动到B板的时间为t，根据运动学规律：
， （2分）
由以上两式解得： t =
。 （2分）
（3）两金属板竖直放置后，液滴在竖直方向作自由落体运动，水平方向在电场力的作用下作匀加速直线运动。设水平方向的加速度为a1，运动到极板的时间为t，根据牛顿第二定律，在水平方向：
= ma1，解得：a1 = g。 （2分）
，解得：t =
。 （2分）
设液滴到达金属板时沿电场方向的速度大小为vx，竖直方向的速度大小为vy则
vx = vy = gt =
， （1分）
则液滴到达极板时的速度大小为
v =
。 （1分）
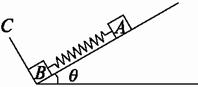
如图13所示，一直角斜槽(两槽面夹角为90°)，对水平面夹角为30°，一个横截面为正方形的物块恰能沿此槽匀速下滑，假定两槽面的材料和表面情况相同，问物块和槽面间的动摩擦因数为多少?