题目内容
6. 一轻质弹簧,两端连接两滑块A和B,已知mA=0.99kg,mB=3kg,放在光滑水平桌面上,开始时弹簧处于原长.现滑块A被水平飞来的质量为mc=10g,速度为400m/s的子弹击中,且没有穿出,如图所示,试求:
一轻质弹簧,两端连接两滑块A和B,已知mA=0.99kg,mB=3kg,放在光滑水平桌面上,开始时弹簧处于原长.现滑块A被水平飞来的质量为mc=10g,速度为400m/s的子弹击中,且没有穿出,如图所示,试求:(1)子弹击中A的瞬间A和B的速度;
(2)以后运动过程中弹簧的最大弹性势能;
(3)B可获得的最大动能.
分析 (1)子弹击中A的瞬间,子弹和A组成的系统水平方向动量守恒,据此可列方程求解A的速度,此过程时间极短,B没有参与,速度仍为零.
(2)以子弹、滑块A、B和弹簧组成的系统为研究对象,当三者速度相等时,系统损失动能最大则弹性势能最,根据动量守恒和功能关系可正确解答.
(3)当弹簧恢复原长时B的动能最大,整个系统相互作用过程中动量守恒,根据功能关系可求出结果.
解答 解:(1)子弹击中滑块A的过程,子弹与滑块A组成的系统动量守恒有:
mCv0=(mC+mA)vA
解得:vA=4m/s
子弹与A作用过程时间极短,B没有参与,速度仍为零,故:vb=0.
故子弹击中A的瞬间A和B的速度分别为:vA=4m/s,vb=0.
(2)对子弹、滑块A、B和弹簧组成的系统,A、B速度相等时弹性势能最大.
根据动量守恒定律和功能关系可得:
mCv0=(mC+mA+mB)v
由此解得:v=1m/s
根据功能关系可得:
${E}_{P}=\frac{1}{2}({m}_{C}+{m}_{A}){{v}_{A}}^{2}-\frac{1}{2}{({m}_{C}+{m}_{A}+{m}_{B})v}^{2}$=6J
故弹簧的最大弹性势能为6J.
(3)设B动能最大时的速度为vB′,A的速度为vA′,则
(mC+mA)vA=(mC+mA)vA′+mBvB′
当弹簧恢复原长时,B的动能最大,根据功能关系有:
$\frac{1}{2}({m}_{C}+{m}_{A}){{v}_{A}}^{2}=\frac{1}{2}{({m}_{C}+{m}_{A}){v}_{A}′}^{2}+\frac{1}{2}{m}_{B}{v}_{B}{′}^{2}$
解得:vB′=2m/s
B获得的最大动能:${E}_{KB}=\frac{1}{2}{m}_{B}{{v}_{B}′}^{2}=6J$
答:(1)子弹击中A的瞬间A的速度为4m/s,B的速度为0;
(2)以后运动过程中弹簧的最大弹性势能为6J;
(3)B可获得的最大动能为6J.
点评 本题考查了动量和能量的综合问题,解答这类问题的关键是弄清最远过程,正确选择状态,然后根据动量和能量守恒列方程求解.

 如图所示,一理想变压器原、副线圈的匝数分别为10:1,原线圈通过一理想电流表A接正弦交流电源,一个二极管和阻值为R的负载电阻串联后接到副线圈的两端.假设该二极管的正向电阻为零,反向电阻为无穷大.用交流电压表测得a、b端和c、d端的电压分别为Uab和Ucd,则( )
如图所示,一理想变压器原、副线圈的匝数分别为10:1,原线圈通过一理想电流表A接正弦交流电源,一个二极管和阻值为R的负载电阻串联后接到副线圈的两端.假设该二极管的正向电阻为零,反向电阻为无穷大.用交流电压表测得a、b端和c、d端的电压分别为Uab和Ucd,则( )| A. | Uab:Ucd=10$\sqrt{2}$:1 | |
| B. | 减小负载电阻的阻值R,电流表的读数变大 | |
| C. | 将二极管短路,电流表的读数变为原来的$\sqrt{2}$倍 | |
| D. | 负载电阻的阻值越小,c、d间的电压Ucd越大 |
 如图所示,在光滑水平面上放置A、B两物体,其中B物体带有不计质量的弹簧静止在水平面内.A物体质量为m,以速度v0逼近B,并压缩弹簧,在压缩的过程中( )
如图所示,在光滑水平面上放置A、B两物体,其中B物体带有不计质量的弹簧静止在水平面内.A物体质量为m,以速度v0逼近B,并压缩弹簧,在压缩的过程中( )| A. | 任意时刻系统的总动量均为mv0 | |
| B. | 任意时刻系统的总动量均为$\frac{m{v}_{0}}{2}$ | |
| C. | 任意一段时间内两物体所受冲量相同 | |
| D. | 当A、B两物体距离最近时,其速度相等 |
| A. | 质点振动方向总是垂直于波传播的方向 | |
| B. | 简谐波沿绳传播,绳上相距半个波长的两个质点振动位移的大小总相等 | |
| C. | 任一振动质点每经过一个周期沿波的传播方向移动一个波长 | |
| D. | 相隔一个周期的两时刻,简谐波的图象不相同 |
 在如图所示的电路中,理想变压器原、副线圈的匝数比为2:1,四个灯泡完全相同,其额定电压为U,若已知灯泡L3和L4恰能正常工作,那么( )
在如图所示的电路中,理想变压器原、副线圈的匝数比为2:1,四个灯泡完全相同,其额定电压为U,若已知灯泡L3和L4恰能正常工作,那么( )| A. | L1和L2都不能正常工作 | B. | L1和L2都不能正常工作 | ||
| C. | 交流电源电压为2U | D. | 交流电源电压为4U |
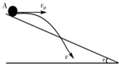 如图所示,从倾角为θ的足够长斜面上的A点,以大小不等的初速度v1和v2(v1>v2)沿水平方向抛出两个小球,两个小球落到斜面上的瞬时速度方向与斜面的夹角分别为α1和α2,则( )
如图所示,从倾角为θ的足够长斜面上的A点,以大小不等的初速度v1和v2(v1>v2)沿水平方向抛出两个小球,两个小球落到斜面上的瞬时速度方向与斜面的夹角分别为α1和α2,则( )| A. | α1=α2 | B. | α1<α2 | C. | α1>α2 | D. | 无法比较 |
| A. | 初速度大的先落地 | B. | 质量大的先落地 | ||
| C. | 无法判断 | D. | 两个石子同时落地 |
 电子感应加速器工作原理如图所示(上图为侧视图、下图为真空室的俯视图),它主要有上、下电磁铁磁极和环形真空室组成.当电磁铁绕组通以变化电流时,产生变化磁场,穿过真空盒所包围的区域内的磁通量随时间变化,这时真空盒空间内就产生感应涡旋电场,电子将在涡旋电场作用下得到加速.在竖直向上的磁感应强度增大过程中,将产生涡旋电场,其电场线是在水平面内一系列沿顺时针方向的同心圆,同一条电场线上各点的场强大小相等,涡旋电场场强与电势差的关系与匀强电场相同.设被加速的电子被“约束”在半径为r的圆周上运动.整个圆面区域内存在有匀强磁场,该匀强磁场的磁感应强度的大小随时间变化的关系式为:B=kt.
电子感应加速器工作原理如图所示(上图为侧视图、下图为真空室的俯视图),它主要有上、下电磁铁磁极和环形真空室组成.当电磁铁绕组通以变化电流时,产生变化磁场,穿过真空盒所包围的区域内的磁通量随时间变化,这时真空盒空间内就产生感应涡旋电场,电子将在涡旋电场作用下得到加速.在竖直向上的磁感应强度增大过程中,将产生涡旋电场,其电场线是在水平面内一系列沿顺时针方向的同心圆,同一条电场线上各点的场强大小相等,涡旋电场场强与电势差的关系与匀强电场相同.设被加速的电子被“约束”在半径为r的圆周上运动.整个圆面区域内存在有匀强磁场,该匀强磁场的磁感应强度的大小随时间变化的关系式为:B=kt.