题目内容
11. 电子感应加速器工作原理如图所示(上图为侧视图、下图为真空室的俯视图),它主要有上、下电磁铁磁极和环形真空室组成.当电磁铁绕组通以变化电流时,产生变化磁场,穿过真空盒所包围的区域内的磁通量随时间变化,这时真空盒空间内就产生感应涡旋电场,电子将在涡旋电场作用下得到加速.在竖直向上的磁感应强度增大过程中,将产生涡旋电场,其电场线是在水平面内一系列沿顺时针方向的同心圆,同一条电场线上各点的场强大小相等,涡旋电场场强与电势差的关系与匀强电场相同.设被加速的电子被“约束”在半径为r的圆周上运动.整个圆面区域内存在有匀强磁场,该匀强磁场的磁感应强度的大小随时间变化的关系式为:B=kt.
电子感应加速器工作原理如图所示(上图为侧视图、下图为真空室的俯视图),它主要有上、下电磁铁磁极和环形真空室组成.当电磁铁绕组通以变化电流时,产生变化磁场,穿过真空盒所包围的区域内的磁通量随时间变化,这时真空盒空间内就产生感应涡旋电场,电子将在涡旋电场作用下得到加速.在竖直向上的磁感应强度增大过程中,将产生涡旋电场,其电场线是在水平面内一系列沿顺时针方向的同心圆,同一条电场线上各点的场强大小相等,涡旋电场场强与电势差的关系与匀强电场相同.设被加速的电子被“约束”在半径为r的圆周上运动.整个圆面区域内存在有匀强磁场,该匀强磁场的磁感应强度的大小随时间变化的关系式为:B=kt.(1)求电子所在圆周上的感生电场场强的大小;
(2)若电子离开电子枪时的速度为v0,求电子被加速一圈之后的速度大小;
(3)在(1)条件下,为了维持电子在恒定的轨道上加速,需要在轨道边缘处外加一个匀强磁场Br,求电子轨道处的磁场Br与轨道内的磁场B应满足什么关系;
(4)若给电磁铁通入正弦交变电流,一个周期内电子能被加速几次.
分析 (1)根据法拉第电磁感应定律,结合磁通量表达式,即可求解;
(2)根据动能定理,结合电场力做功,即可求解;
(3)根据运动的合成与分解,由牛顿第二定律,结合洛伦兹力与向心力表达式,即可求解;
(4)根据在不同时间内,分析电子受力与运动情况,从而即可求解.
解答 解:(1)设被加速的电子被“约束”在半径为r的圆周上运动,在半径为r的圆面上,通过的磁通量为Φ=BπR2,B是整个圆面区域内的磁感应强度,电子所在圆周上的感生电场场强为E′.
根据法拉第电磁感应定律E=$\frac{△Φ}{△t}$ 得,$E′×2πr=\frac{△B}{△t}π{r}^{2}$
感生电场的大小:$E′=\frac{kr}{2}$
(2)根据动能定理,则有:$E′e×2πr=\frac{m({v}^{2}-{v}_{0}^{2})}{2}$
解得:v=$\sqrt{\frac{2kπe{r}^{2}}{m}+{v}_{0}^{2}}$
(3)设电子在半径为r的轨道上运动时,轨道所在处的磁感应强度为Br,而在半径为r的圆面区域内的磁感应强度为B,维持电子在恒定的轨道上加速时,由牛顿第二定律得
在切线方向:$eE′=ma=m\frac{△v}{△t}$,
将$E′=\frac{r}{2}\frac{△B}{△t}$
代入$e•\frac{r}{2}•\frac{△B}{△t}$=m$\frac{△v}{△t}$ ①
在半径方向:$ev{B}_{r}=m\frac{{v}^{2}}{r}$
化简得$e{B}_{r}=m\frac{v}{r}$ ②
将②式对时间微分得$e\frac{△{B}_{r}}{△t}=\frac{m}{r}•\frac{△v}{△t}$ ③
由①③得${B}_{r}=\frac{B}{2}$
即电子轨道处的磁感应强度为轨道内部磁感应强度的一半.
(4)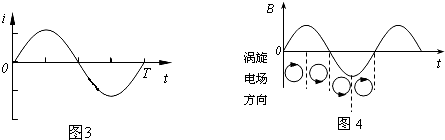
给电磁铁通入交变电流如图3所示,从而产生变化的磁场,变化规律如图4所示(以图乙中所标电流产生磁场的方向为正方向),要使电子能被逆时针(从上往下看,以下同)加速,
一方面感生电场应是顺时针方向,即在磁场的第一个或第四个$\frac{1}{4}$周期内加速电子;
而另一方面电子受到的洛仑兹力应指向圆心,只有磁场的第一或第二个$\frac{1}{4}$周期才满足.
所以只有在磁场变化的第一个$\frac{1}{4}$周期内,电子才能在感生电场的作用下不断加速.
因此,一个周期内电子只能被加速一次.
答:(1)电子所在圆周上的感生电场场强的大小$\frac{kr}{2}$;
(2)若电子离开电子枪时的速度为v0,电子被加速一圈之后的速度大小$\sqrt{\frac{2kπe{r}^{2}}{m}+{v}_{0}^{2}}$;
(3)在(1)条件下,为了维持电子在恒定的轨道上加速,需要在轨道边缘处外加一个匀强磁场Br,电子轨道处的磁感应强度为轨道内部磁感应强度的一半;
(4)若给电磁铁通入正弦交变电流,一个周期内电子能被加速一次.
点评 考查属于力电综合题,掌握牛顿第二定律与运动学公式的应用,注意运动的合成与分解,同时掌握洛伦兹力与向心力表达式.关键还是画出电子的运动轨迹.

| A. | 1:4 | B. | 2:3 | C. | 4:9 | D. | 9:16 |
| A. | X+${\;}_{7}^{14}$H→${\;}_{8}^{17}$O+${\;}_{1}^{1}$H中,X表示${\;}_{2}^{3}$He | |
| B. | ${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n是轻核聚变 | |
| C. | 半衰期与原子所处的化学状态无关 | |
| D. | β衰变中产生的β射线实际上是原子的核外电子挣脱原子核的束缚而形成的 |
| A. | 它处于平衡状态,且具有一定的高度 | |
| B. | 它的加速度小于9.8m/s2 | |
| C. | 它的速度等于7.9km/s | |
| D. | 它的周期是24h,且轨道平面与赤道平面重合 |
 如图所示,飞行器P在赤道面绕地球做匀速圆周运动,运动方向与地球自转方向一致,已知地球相对飞行器P的张角为θ,地球的半径为R,地球的自转周期为T0,飞行器P的公转周期为T,万有引力常量为G,当地面通信基站观测到飞行器时,两者就可以进行点对点直接通信,忽略信号的传输时间.下列说法正确的是( )
如图所示,飞行器P在赤道面绕地球做匀速圆周运动,运动方向与地球自转方向一致,已知地球相对飞行器P的张角为θ,地球的半径为R,地球的自转周期为T0,飞行器P的公转周期为T,万有引力常量为G,当地面通信基站观测到飞行器时,两者就可以进行点对点直接通信,忽略信号的传输时间.下列说法正确的是( )| A. | 地球相对飞行器P的张角θ越小,飞行器P的运行周期越大 | |
| B. | 飞行器P的轨道半径r=Rsin$\frac{θ}{2}$ | |
| C. | 地球的质量M=$\frac{{4{π^2}{R^3}}}{{G{T^2}{{sin}^3}\frac{θ}{2}}}$ | |
| D. | 赤道上固定的一个地面通信基站在T0的时间内可以与飞行器通信的总时间为$\frac{(π-θ)}{2π}\frac{{{T_0}^2}}{{{T_0}-T}}$ |
| A. | 升降机以0.8g的加速度加速上升 | B. | 升降机以0.2g的加速度加速上升 | ||
| C. | 升降机以0.2g的加速度减速上升 | D. | 升降机以0.8g的加速度减速下降 |
 一轻质弹簧,两端连接两滑块A和B,已知mA=0.99kg,mB=3kg,放在光滑水平桌面上,开始时弹簧处于原长.现滑块A被水平飞来的质量为mc=10g,速度为400m/s的子弹击中,且没有穿出,如图所示,试求:
一轻质弹簧,两端连接两滑块A和B,已知mA=0.99kg,mB=3kg,放在光滑水平桌面上,开始时弹簧处于原长.现滑块A被水平飞来的质量为mc=10g,速度为400m/s的子弹击中,且没有穿出,如图所示,试求: 如图所示,匀强磁场磁感应强度大小B=0.50T,矩形线圈的匝数N=100匝,边长Lab=0.20m,Lac=0.10m,线圈以300rad/s的角速度匀速转动.若线圈的总电阻r=1Ω,线圈外接电阻R=9Ω.
如图所示,匀强磁场磁感应强度大小B=0.50T,矩形线圈的匝数N=100匝,边长Lab=0.20m,Lac=0.10m,线圈以300rad/s的角速度匀速转动.若线圈的总电阻r=1Ω,线圈外接电阻R=9Ω.