题目内容
15.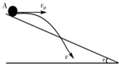 如图所示,从倾角为θ的足够长斜面上的A点,以大小不等的初速度v1和v2(v1>v2)沿水平方向抛出两个小球,两个小球落到斜面上的瞬时速度方向与斜面的夹角分别为α1和α2,则( )
如图所示,从倾角为θ的足够长斜面上的A点,以大小不等的初速度v1和v2(v1>v2)沿水平方向抛出两个小球,两个小球落到斜面上的瞬时速度方向与斜面的夹角分别为α1和α2,则( )| A. | α1=α2 | B. | α1<α2 | C. | α1>α2 | D. | 无法比较 |
分析 平抛运动落在斜面上时,竖直方向的位移和水平方向上位移比值一定,根据该规律求出平抛运动的时间,从而求出落在斜面上时,速度与水平方向的夹角,速度方向与斜面的夹角等于速度与水平方向的夹角减去斜面的倾角.
解答 解:根据$tanθ=\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}$得:t=$\frac{2{v}_{0}tanθ}{g}$,
则落在斜面上时竖直方向上的分速度为:vy=gt=2v0tanθ.
设速度与水平方向的夹角为α,有$tanα=\frac{{v}_{y}}{{v}_{0}}=2tanθ$.知落在斜面上时,速度与水平方向的夹角与初速度无关,则小球与水平方向的夹角相同,因为速度方向与斜面的夹角等于速度与水平方向的夹角减去斜面的倾角,所以α1=α2.故A正确,B、C、D错误.
故选:A.
点评 解决本题的关键掌握平抛运动的规律,知道平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动.

练习册系列答案
相关题目
5.物体受几个外力作用下恰作匀速直线运动,如果突然撤去其中的一个力F2,则它可能做( )
| A. | 匀速直线运动 | B. | 匀加速直线运动 | C. | 匀减速直线运动 | D. | 匀变速曲线运动 |
3. 如图所示,飞行器P在赤道面绕地球做匀速圆周运动,运动方向与地球自转方向一致,已知地球相对飞行器P的张角为θ,地球的半径为R,地球的自转周期为T0,飞行器P的公转周期为T,万有引力常量为G,当地面通信基站观测到飞行器时,两者就可以进行点对点直接通信,忽略信号的传输时间.下列说法正确的是( )
如图所示,飞行器P在赤道面绕地球做匀速圆周运动,运动方向与地球自转方向一致,已知地球相对飞行器P的张角为θ,地球的半径为R,地球的自转周期为T0,飞行器P的公转周期为T,万有引力常量为G,当地面通信基站观测到飞行器时,两者就可以进行点对点直接通信,忽略信号的传输时间.下列说法正确的是( )
 如图所示,飞行器P在赤道面绕地球做匀速圆周运动,运动方向与地球自转方向一致,已知地球相对飞行器P的张角为θ,地球的半径为R,地球的自转周期为T0,飞行器P的公转周期为T,万有引力常量为G,当地面通信基站观测到飞行器时,两者就可以进行点对点直接通信,忽略信号的传输时间.下列说法正确的是( )
如图所示,飞行器P在赤道面绕地球做匀速圆周运动,运动方向与地球自转方向一致,已知地球相对飞行器P的张角为θ,地球的半径为R,地球的自转周期为T0,飞行器P的公转周期为T,万有引力常量为G,当地面通信基站观测到飞行器时,两者就可以进行点对点直接通信,忽略信号的传输时间.下列说法正确的是( )| A. | 地球相对飞行器P的张角θ越小,飞行器P的运行周期越大 | |
| B. | 飞行器P的轨道半径r=Rsin$\frac{θ}{2}$ | |
| C. | 地球的质量M=$\frac{{4{π^2}{R^3}}}{{G{T^2}{{sin}^3}\frac{θ}{2}}}$ | |
| D. | 赤道上固定的一个地面通信基站在T0的时间内可以与飞行器通信的总时间为$\frac{(π-θ)}{2π}\frac{{{T_0}^2}}{{{T_0}-T}}$ |
20.在升降机内,一个人站在磅秤上,发现自己的体重减轻了20%,于是他做出了下列判断中正确的是( )
| A. | 升降机以0.8g的加速度加速上升 | B. | 升降机以0.2g的加速度加速上升 | ||
| C. | 升降机以0.2g的加速度减速上升 | D. | 升降机以0.8g的加速度减速下降 |
7.一辆质量为M的超重车,行驶上半径为R的圆弧形拱桥顶点,已知此处桥面能承受的最大压力只是车重的0.75倍,要使车能安全沿桥面行驶,则此处车的速度v应在( )
| A. | 0<v<$\sqrt{gR}$ | B. | 0<v<$\frac{1}{2}\sqrt{gR}$ | C. | $\frac{1}{2}\sqrt{gR}$<v<$\sqrt{gR}$ | D. | $\frac{1}{4}\sqrt{gR}$<v<$\frac{1}{2}\sqrt{gR}$ |
4.在“探究功与速度变化的关系”的实验中,关于橡皮筋做的功,下列说法正确的是( )
| A. | 橡皮筋做的功可以直接测量 | |
| B. | 通过增加橡皮筋的条数可以使橡皮筋对小车做的功成整数倍增加 | |
| C. | 橡皮筋在小车运动的全程中始终做功 | |
| D. | 把橡皮筋拉伸为原来的两倍,橡皮筋做功也增加为原来的两倍 |
5. 如图所示,小球从高处下落到竖直放置的轻弹簧上,若不计空气阻力,从弹簧被压缩开始到弹簧被压缩至最短的过程中,下列关于能量的叙述中正确的是( )
如图所示,小球从高处下落到竖直放置的轻弹簧上,若不计空气阻力,从弹簧被压缩开始到弹簧被压缩至最短的过程中,下列关于能量的叙述中正确的是( )
 如图所示,小球从高处下落到竖直放置的轻弹簧上,若不计空气阻力,从弹簧被压缩开始到弹簧被压缩至最短的过程中,下列关于能量的叙述中正确的是( )
如图所示,小球从高处下落到竖直放置的轻弹簧上,若不计空气阻力,从弹簧被压缩开始到弹簧被压缩至最短的过程中,下列关于能量的叙述中正确的是( )| A. | 小球的重力势能和动能之和总保持不变 | |
| B. | 小球的重力势能和动能之和一直减小 | |
| C. | 小球的重力势能与弹簧的弹性势能之和先减小后增大 | |
| D. | 小球和弹簧组成系统的机械能守恒 |
 一轻质弹簧,两端连接两滑块A和B,已知mA=0.99kg,mB=3kg,放在光滑水平桌面上,开始时弹簧处于原长.现滑块A被水平飞来的质量为mc=10g,速度为400m/s的子弹击中,且没有穿出,如图所示,试求:
一轻质弹簧,两端连接两滑块A和B,已知mA=0.99kg,mB=3kg,放在光滑水平桌面上,开始时弹簧处于原长.现滑块A被水平飞来的质量为mc=10g,速度为400m/s的子弹击中,且没有穿出,如图所示,试求: 在研究某些物理问题时,有很多物理量难以直接测量,我们可以根据物理量之间的定量关系和各种效应,把不容易测量的物理量转化成易于测量的物理量.载流导体板垂直置于匀强磁场中,当电流通过导体板时,在导体板这两个表面之间就会形成稳定的电势差,这种现象称为霍尔效应.利用霍尔效应可以测量磁场的磁感应强度.半导体材料硅中掺砷后成为N型半导体,它的自由电子的浓度大大增加,导电能力也大大增加.一块N型半导体的样品的体积为a?b?c,A′、C、A、C′为其四个侧面,如图所示.已知半导体样品单位体积中的电子数为n,电子的电荷量为e.将半导体样品放在匀强磁场中,磁场方向沿Z轴正方向,并沿x方向通有电流I.试分析求解:
在研究某些物理问题时,有很多物理量难以直接测量,我们可以根据物理量之间的定量关系和各种效应,把不容易测量的物理量转化成易于测量的物理量.载流导体板垂直置于匀强磁场中,当电流通过导体板时,在导体板这两个表面之间就会形成稳定的电势差,这种现象称为霍尔效应.利用霍尔效应可以测量磁场的磁感应强度.半导体材料硅中掺砷后成为N型半导体,它的自由电子的浓度大大增加,导电能力也大大增加.一块N型半导体的样品的体积为a?b?c,A′、C、A、C′为其四个侧面,如图所示.已知半导体样品单位体积中的电子数为n,电子的电荷量为e.将半导体样品放在匀强磁场中,磁场方向沿Z轴正方向,并沿x方向通有电流I.试分析求解: