题目内容
 光滑水平面上放有如图所示的用绝缘材料制成的“┙”型滑板,(平面部分足够长),质量为4m,距滑板的A壁为L1距离的B处放有一质量为m,电量为+q的大小不计的小物体,物体与板面的摩擦不计,整个装置处于场强为E的匀强电场中,初始时刻,滑板与物体都静止,试求:
光滑水平面上放有如图所示的用绝缘材料制成的“┙”型滑板,(平面部分足够长),质量为4m,距滑板的A壁为L1距离的B处放有一质量为m,电量为+q的大小不计的小物体,物体与板面的摩擦不计,整个装置处于场强为E的匀强电场中,初始时刻,滑板与物体都静止,试求:(1)释放小物体,第一次与滑板A壁碰前物体的速度v1多大?
(2)若物体与A壁碰后相对水平面的速度大小为碰前的
| 3 | 5 |
(3)物体从开始运动到第二次碰撞前,电场力做功为多大?
分析:(1)释放小物体,B受到水平向右的电场力作用而做匀加速直线运动,由于BA间没有摩擦,A处于静止,根据动能定理求解小物体第一次与滑板A壁碰前物体的速度v1.
(2)物体B与A碰撞过程,动量守恒,由动量守恒定律求出碰撞后A的速度大小和方向,确定出B的速度方向.碰撞后A向右做匀速运动直到与物体第二次碰撞之前,碰撞后B反弹向左做匀减速运动,当两者的位移相等时,发生第二碰撞,由运动学公式列出B的速度与时间的关系式,根据位移关系再列出位移与时间的关系式,联立即可求出物体在第二次跟A壁碰撞之前瞬时,滑板的速度v和物体的速度v2.
(3)根据运动学公式求出两次碰撞之间的位移,即可求得电场力做功.
(2)物体B与A碰撞过程,动量守恒,由动量守恒定律求出碰撞后A的速度大小和方向,确定出B的速度方向.碰撞后A向右做匀速运动直到与物体第二次碰撞之前,碰撞后B反弹向左做匀减速运动,当两者的位移相等时,发生第二碰撞,由运动学公式列出B的速度与时间的关系式,根据位移关系再列出位移与时间的关系式,联立即可求出物体在第二次跟A壁碰撞之前瞬时,滑板的速度v和物体的速度v2.
(3)根据运动学公式求出两次碰撞之间的位移,即可求得电场力做功.
解答:解:(1)由动能定理得 qEL1=
m
得 v1=
(2)若物体碰后仍沿原来方向运动,碰后滑板的速度为v,由动量守恒得
mv1=m?
v1+4mv
解得,v=
<
v1,由于B与A同向运动,故不可能,
∴物块碰后必反弹,速度为v1′=-
v1
根据动量守恒定律得
mv1=-m?
v1+4mv 解得 v=
v1
(2)由于碰后滑板匀速运动直至与物体第二碰撞之前,故物体与A第二次碰前,滑板的速度为 v=
v1=
物体与A壁第二碰前,设物块的速度为v2,
v2=v1′+at
两物体第二次相碰时,位移相等,则有
vt=v1′+
at2
得 v=v1′+
at,
又a=
联立解得,v2=
(3)设物体在两次碰撞之间位移为S
由
-
=2aS
得 S=
=
=
故物体从开始运动到第二次碰撞前,电场力做功为 W=qE(L1+S)=
qEL1.
答:
(1)释放小物体,第一次与滑板A壁碰前物体的速度v1是
.
(2)物体在第二次跟A壁碰撞之前瞬时,滑板的速度v和物体的速度v2分别为
和
.
(3)物体从开始运动到第二次碰撞前,电场力做功为
qEL1.
| 1 |
| 2 |
| v | 2 1 |
|
(2)若物体碰后仍沿原来方向运动,碰后滑板的速度为v,由动量守恒得
mv1=m?
| 3 |
| 5 |
解得,v=
| v1 |
| 10 |
| 3 |
| 5 |
∴物块碰后必反弹,速度为v1′=-
| 3 |
| 5 |
根据动量守恒定律得
mv1=-m?
| 3 |
| 5 |
| 2 |
| 5 |
(2)由于碰后滑板匀速运动直至与物体第二碰撞之前,故物体与A第二次碰前,滑板的速度为 v=
| 2 |
| 5 |
| 2 |
| 5 |
|
物体与A壁第二碰前,设物块的速度为v2,
v2=v1′+at
两物体第二次相碰时,位移相等,则有
vt=v1′+
| 1 |
| 2 |
得 v=v1′+
| 1 |
| 2 |
又a=
| qE |
| m |
联立解得,v2=
| 7 |
| 5 |
|
(3)设物体在两次碰撞之间位移为S
由
| v | 2 2 |
| v | ′2 1 |
得 S=
| ||||
| 2a |
[(
| ||||||
2?
|
4m
| ||
| 5qE |
故物体从开始运动到第二次碰撞前,电场力做功为 W=qE(L1+S)=
| 13 |
| 5 |
答:
(1)释放小物体,第一次与滑板A壁碰前物体的速度v1是
|
(2)物体在第二次跟A壁碰撞之前瞬时,滑板的速度v和物体的速度v2分别为
| 2 |
| 5 |
|
| 7 |
| 5 |
|
(3)物体从开始运动到第二次碰撞前,电场力做功为
| 13 |
| 5 |
点评:本题运用程序法按时间顺序分析物体运动的过程,难点是判断第一次碰撞后B的速度方向,抓住碰撞后同向运动的物体,后面物体的速度不可能大于前面物体的速度.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
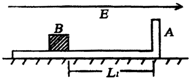 (2003?肇庆模拟)光滑水平面上放有如图所示的用绝缘材料制成的L形滑板(平面部分足够长),质量为4m,距滑板的A壁为L距离的B处放有一质量为m,电量为+q的大小不计的小物体,物体与板面的摩擦不计,整个装置处于场强为E的匀强电场中.初始时刻,滑块与物体都静止,试问:
(2003?肇庆模拟)光滑水平面上放有如图所示的用绝缘材料制成的L形滑板(平面部分足够长),质量为4m,距滑板的A壁为L距离的B处放有一质量为m,电量为+q的大小不计的小物体,物体与板面的摩擦不计,整个装置处于场强为E的匀强电场中.初始时刻,滑块与物体都静止,试问: ”型滑板,(平面部分足够长),质量为4m,距滑板的A壁为L1距离的B处放有一质量为m,电量为+q的大小不计的小物体,物体与板面的摩擦不计,整个装置处于场强为E的匀强电场中,初始时刻,滑板与物体都静止,试求:
”型滑板,(平面部分足够长),质量为4m,距滑板的A壁为L1距离的B处放有一质量为m,电量为+q的大小不计的小物体,物体与板面的摩擦不计,整个装置处于场强为E的匀强电场中,初始时刻,滑板与物体都静止,试求:
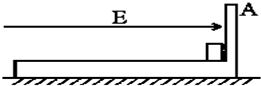 在光滑水平面上放有如图所示的用绝缘材料制成的“┙”型滑板,其质量为m1=40kg,在滑板右端A壁左侧有一质量为m2=10kg,带电荷量为q=+2C的小铁块,在小铁块与A壁之间夹有一小堆火药,整个装置始终处于场强为E=10N/C的水平向右的匀强电场中.初始时刻,使滑板与小铁块都处于静止,现点燃火药.设火药爆炸时有100J的能量转化为滑板和小铁块的机械能,滑板水平部分足够长,小铁块和火药的体积大小、小铁块与滑板面的摩擦均不计,火药爆炸的作用力远大于电场力,爆炸后,滑板和小铁块质量、形状均不变,小铁块没有电量损失,小铁块始终未脱离滑板.试求:
在光滑水平面上放有如图所示的用绝缘材料制成的“┙”型滑板,其质量为m1=40kg,在滑板右端A壁左侧有一质量为m2=10kg,带电荷量为q=+2C的小铁块,在小铁块与A壁之间夹有一小堆火药,整个装置始终处于场强为E=10N/C的水平向右的匀强电场中.初始时刻,使滑板与小铁块都处于静止,现点燃火药.设火药爆炸时有100J的能量转化为滑板和小铁块的机械能,滑板水平部分足够长,小铁块和火药的体积大小、小铁块与滑板面的摩擦均不计,火药爆炸的作用力远大于电场力,爆炸后,滑板和小铁块质量、形状均不变,小铁块没有电量损失,小铁块始终未脱离滑板.试求: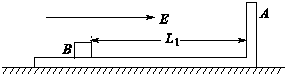 体,求:
体,求: