题目内容
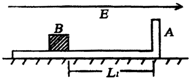 (2003?肇庆模拟)光滑水平面上放有如图所示的用绝缘材料制成的L形滑板(平面部分足够长),质量为4m,距滑板的A壁为L距离的B处放有一质量为m,电量为+q的大小不计的小物体,物体与板面的摩擦不计,整个装置处于场强为E的匀强电场中.初始时刻,滑块与物体都静止,试问:
(2003?肇庆模拟)光滑水平面上放有如图所示的用绝缘材料制成的L形滑板(平面部分足够长),质量为4m,距滑板的A壁为L距离的B处放有一质量为m,电量为+q的大小不计的小物体,物体与板面的摩擦不计,整个装置处于场强为E的匀强电场中.初始时刻,滑块与物体都静止,试问:(1)释放小物体,第一次与滑板A壁碰前物体的速度υ1多大?
(2)若物体与A壁碰后相对水平面的速率为碰前速率的
| 3 | 5 |
(3)物体从开始运动到第二次碰撞前,电场力做的功为多大?(设碰撞所经历时间极短)
分析:(1)物体在电场力作用下做匀加速运动,电场力做功qEl,由动能定理求解第一次与滑板A端相碰前瞬间的速度大小;
(2)小物体与滑板碰撞过程中系统合外力为零,由动量守恒定律求出滑板被碰后的速度大小;
(3)对整个过程运用动能定理即可求解.
(2)小物体与滑板碰撞过程中系统合外力为零,由动量守恒定律求出滑板被碰后的速度大小;
(3)对整个过程运用动能定理即可求解.
解答:解:(1)对物体,根据动能定理,有qEL1=
mv12,得 v1=
.
(2)物体与滑板碰撞前后动量守恒,设物体第一次与滑板碰后的速度为v1′;滑板的速度为v,则
mv1=mv1′+4mv.
若v1′=
v1,则v=
v1,因为v1′>v,不符合实际,
故应取v1′=-
v1,则v=
v1=
.
在物体第一次与A壁碰后到第二次与A壁碰前,物体做匀变速运动,滑板做匀速运动,在这段时间内,两者相对于水平面的位移相同.
∴
(v2+v1′)t=v?t,
即v2=
v1=
.
(3)对整个过程运用动能定理得;
电场力做功W=
mv12+(
mv22-
mv1′2)=
qEL1.
答:(1)释放小物体,第一次与滑板A壁碰前物体的速度为
;
(2)若物体与A壁碰后相对水平面的速率为碰前速率的
,则物体在第二次跟A壁碰撞之前,滑板相对于水平面的速度为
,物体相对于水平面的速度υ2分别为
;
(3)物体从开始运动到第二次碰撞前,电场力做的功为
qEL1.
| 1 |
| 2 |
|
(2)物体与滑板碰撞前后动量守恒,设物体第一次与滑板碰后的速度为v1′;滑板的速度为v,则
mv1=mv1′+4mv.
若v1′=
| 3 |
| 5 |
| 1 |
| 10 |
故应取v1′=-
| 3 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
|
在物体第一次与A壁碰后到第二次与A壁碰前,物体做匀变速运动,滑板做匀速运动,在这段时间内,两者相对于水平面的位移相同.
∴
| 1 |
| 2 |
即v2=
| 7 |
| 5 |
| 7 |
| 5 |
|
(3)对整个过程运用动能定理得;
电场力做功W=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 13 |
| 5 |
答:(1)释放小物体,第一次与滑板A壁碰前物体的速度为
|
(2)若物体与A壁碰后相对水平面的速率为碰前速率的
| 3 |
| 5 |
| 2 |
| 5 |
|
| 7 |
| 5 |
|
(3)物体从开始运动到第二次碰撞前,电场力做的功为
| 13 |
| 5 |
点评:本题主要考查了动量守恒定律及动能定理的应用,要求同学们能正确分析出物体碰前、碰后的运动情况,难度适中.

练习册系列答案
相关题目
 (2003?肇庆模拟)用如图所示的装置进行以下实验:
(2003?肇庆模拟)用如图所示的装置进行以下实验: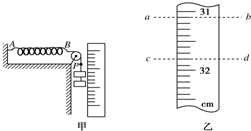 (2003?肇庆模拟)用如图甲所示的装置测定弹簧的劲度系数,被测弹簧一端固定于A点,另一端B用细绳绕过定滑轮挂钩码,旁边竖直固定一最小刻度为mm的刻度尺,当挂两个钩码时,绳上一定点P对应刻度如图乙中ab虚线所示,再增加一个钩码后,P点对应刻度如图乙中cd虚线所示,已知每个钩码质量为50g,重力加速度g=9.8m/s2,则被测弹簧的劲度系数为
(2003?肇庆模拟)用如图甲所示的装置测定弹簧的劲度系数,被测弹簧一端固定于A点,另一端B用细绳绕过定滑轮挂钩码,旁边竖直固定一最小刻度为mm的刻度尺,当挂两个钩码时,绳上一定点P对应刻度如图乙中ab虚线所示,再增加一个钩码后,P点对应刻度如图乙中cd虚线所示,已知每个钩码质量为50g,重力加速度g=9.8m/s2,则被测弹簧的劲度系数为 (2003?肇庆模拟)一个质量m=0.20kg的小球系于轻质弹簧的一端,且套在光滑竖立的圆环上,弹簧的上端固定于环的最高点A,环的半径R=0.5m,弹簧的原长L0=0.50m,劲度系数为4.8N/m,如图所示,若小球从图中所示位置B点由静止开始滑动到最低点C时,弹簧的弹性势能Ep弹=0.60J.
(2003?肇庆模拟)一个质量m=0.20kg的小球系于轻质弹簧的一端,且套在光滑竖立的圆环上,弹簧的上端固定于环的最高点A,环的半径R=0.5m,弹簧的原长L0=0.50m,劲度系数为4.8N/m,如图所示,若小球从图中所示位置B点由静止开始滑动到最低点C时,弹簧的弹性势能Ep弹=0.60J. (2003?肇庆模拟)在把电流表改装成电压表的实验中,测定电流表的内阻时,备有如下器材:
(2003?肇庆模拟)在把电流表改装成电压表的实验中,测定电流表的内阻时,备有如下器材: