Question

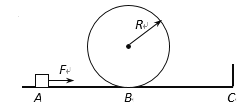
【题目】如图所示，半径R=0.3m的竖直圆槽型光滑轨道与水平轨道AC相切于B点，水平轨道的C点固定有竖直挡板，轨道上的A点静置有一质量m=1kg的小物块(可视为质点)．现给小物块施加一大小为F=25N、方向水平向右的恒定拉力，使小物块沿水平轨道AC向右运动，当运动到AB之间的D点(图中未画出)时撤去拉力，小物块继续滑行到B点后进入竖直圆槽轨道做圆周运动，当物块运动到最高点时，由压力传感器测出小物块对轨道最高点的压力为10/3N．已知水平轨道AC长为2m，B为AC的中点，小物块与AB段间的动摩擦因数=0.45，重力加速度g=10．求：

⑴小物块运动到B点时的速度大小；

⑵拉力F作用在小物块上的时间t．

Answer 1

【答案】(1)4m/s；(2)0.22s

【解析】

(1)小物块运动到轨道最高点时，由牛顿第二定律得：

可得：=2m/s

物块从B运动到轨道最高点的过程，由机械能守恒定律得：

可得：=4m/s

(2)小物块从运动到B点的过程，运用动能定理得：

根据牛顿第二定律得：

由运动学公式有：

联立解得：t=≈0.22s