题目内容
【题目】如图所示，轻质弹簧一端固定，另一端与质量为m、套在粗糙竖直固定杆A处的圆环相连，弹簧水平且处于原长．圆环从A处由静止释放后，经过B处速度最大，到达C处（AC=h）时速度减为零．若在此时给圆环一个竖直向上的速度v，它恰好能回到A点．弹簧始终在弹性限度内，重力加速度为g，则圆环（ ）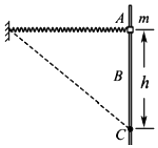
A.下滑过程中，加速度一直增大
B.上下两次经过B点的速度大小相等
C.下滑过程中，克服摩擦力做的功为 
mv2
D.在C处弹簧的弹性势能为 mgh﹣ mv2
【答案】C,D
【解析】解：A、圆环从A处由静止开始下滑，经过B处的速度最大，到达C处的速度为零，所以圆环先做加速运动，再做减速运动，经过B处的速度最大，加速度为零，所以加速度先减小，后增大，故A错误
B、研究圆环从A处由静止开始下滑到B过程，运用动能定理列出等式
mgh′﹣W′f﹣W′弹= 
﹣0
研究圆环从B处上滑到A的过程，运用动能定理列出等式
﹣mgh′﹣W′f+W′弹=0﹣ 
即得 mgh′+W′f﹣W′弹=
由于W′f＞0，所以 ＞ ，可知上滑经过B的速度大于下滑经过B的速度，故B错误．
C、研究圆环从A处由静止开始下滑到C过程，运用动能定理列出等式
mgh﹣Wf﹣W弹=0﹣0=0
在C处获得一竖直向上的速度v，恰好能回到A，运用动能定理列出等式
﹣mgh+W弹﹣Wf=0﹣ 
mv2
解得：下滑过程中，克服摩擦力做的功Wf= 
mv2，故C正确．
D、由上解得 W弹= mv2﹣mgh，所以在C处，弹簧的弹性势能为mgh﹣ mv2，故D正确；
故选：CD
根据圆环的运动情况分析下滑过程中加速度的变化；研究圆环从A处由静止开始下滑到C和在C处获得一竖直向上的速度v，恰好能回到A两个过程，运用动能定理列出等式求解；研究圆环从A处由静止开始下滑到B过程和圆环从B处上滑到A的过程，运用动能定理列出等式，比较两次经过B点时速度大小．
